题目内容
【题目】如图,已知 BF=CE,∠B=∠E,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
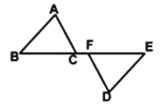
A. AB=DE B. AC∥DF C. ∠A=∠D D. AC=DF
【答案】D
【解析】
根据全等三角形的判定定理分别进行分析即可.
A.∵BF=CE,∴BF-CF=CE-CF,即BC=EF.
∵∠B=∠E,AB=DE,∴ABC≌DEF(SAS),故A不符合题意.
B.∵AC∥DF,∴∠ACE=∠DFC,∴∠ACB=∠DFE(等角的补角相等)
∵BF=CE,∠B=∠E,∴BF-CF=CE-CF,即BC=EF,∴ABC≌DEF(ASA),故B不符合题意.
C.∵BF=CE,∴BF-CF=CE-CF,即BC=EF.
而∠A=∠D,∠B=∠E,∴ABC≌DEF(AAS),故C不符合题意.
D.∵BF=CE,∴BF-CF=CE-CF,即BC=EF,而AC=DF,∠B=∠E,三角形中,有两边及其中一边的对角对应相等,不能判断两个三角形全等,故D符合题意.
故选D.

练习册系列答案
相关题目