题目内容
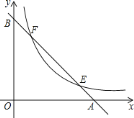
【题目】如图,已知直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() ,
,![]() 两点,与双曲线
两点,与双曲线![]() 交于
交于![]() ,
,![]() 两点,若
两点,若![]() ,则
,则![]() 的值是________.
的值是________.
【答案】![]()
【解析】
试题作FH⊥x轴,EC⊥y轴,FH与EC交于D,先利用一次函数图象上点的坐标特征得到A(2,0),B(0, 2),易得△AOB为等腰直角三角形,则AB=![]() OA=2
OA=2![]() ,所以EF=
,所以EF=![]() AB=
AB=![]() ,且△DEF为等腰直角三角形,则FD=DE=
,且△DEF为等腰直角三角形,则FD=DE=![]() EF=1;设F点坐标为(t,-t+2),则E点坐标为(t+1,-t+1),根据反比例函数图象上点的坐标特征得到t(-t+2)=(t+1)(-t+1),解得t=
EF=1;设F点坐标为(t,-t+2),则E点坐标为(t+1,-t+1),根据反比例函数图象上点的坐标特征得到t(-t+2)=(t+1)(-t+1),解得t=![]() ,这样可确定E点坐标为(
,这样可确定E点坐标为(![]() ,
,![]() ),然后根据反比例函数图象上点的坐标特征得到k=
),然后根据反比例函数图象上点的坐标特征得到k=![]() ×
×![]() .
.
试题解析:作FH⊥x轴,EC⊥y轴,FH与EC交于D,如图,
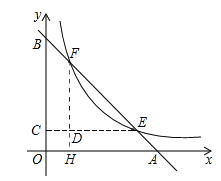
A点坐标为(2,0),B点坐标为(0,2),OA=OB,
∴△AOB为等腰直角三角形,
∴AB=![]() OA=2
OA=2![]() ,
,
∴EF=![]() AB=
AB=![]() ,
,
∴△DEF为等腰直角三角形,
∴FD=DE=![]() EF=1;
EF=1;
设F点横坐标为t,代入y=-x+2,则纵坐标是-t+2,则F的坐标是:(t,-t+2),E点坐标为(t+1,-t+1),
∴t(-t+2)=(t+1)(-t+1),解得t=![]()
∴E点坐标为(![]() ,
,![]() )
)
∴k=![]() ×
×![]() =
=![]() .
.

练习册系列答案
相关题目



