题目内容
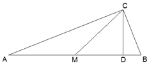
【题目】如图在△ABC中,∠ACB=90°,CD⊥AB,M是AB的中点,若CM=2CD,则下列结论中错误的是( )
A.CB=![]() ABB.CD=
ABB.CD=![]() MDC.∠BCM=75°D.∠ACM=15°
MDC.∠BCM=75°D.∠ACM=15°
【答案】A
【解析】
首先根据直角三角形斜边中线定理得出CM=AM=BM,进而得出∠MAC=∠ACM=![]() ∠CMD,再由CD⊥AB, CM=2CD,得出∠CMD=30°,∠MAC=∠ACM=15°,进而得出CD=
∠CMD,再由CD⊥AB, CM=2CD,得出∠CMD=30°,∠MAC=∠ACM=15°,进而得出CD=![]() MD,∠BCM=75°,即可判定B、C、D正确,A中CB≠
MD,∠BCM=75°,即可判定B、C、D正确,A中CB≠![]() AB,即可得解.
AB,即可得解.
∵在△ABC中,∠ACB=90°, M是AB的中点,
∴CM=AM=BM
∴∠MAC=∠ACM=![]() ∠CMD
∠CMD
又∵CD⊥AB, CM=2CD,
∴∠CMD=30°,∠MAC=∠ACM=15°
∴CD=![]() MD,∠BCM=75°
MD,∠BCM=75°
∴B、C、D正确;
∴CB≠![]() AB,
AB,
∴A错误
故答案为A.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | | 8 | 0.4 |
乙 | | 9 | | 3.2 |
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).