Question

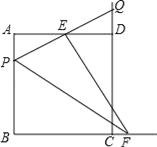
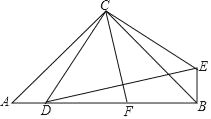
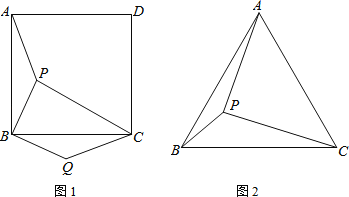
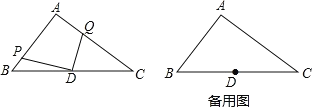
【题目】如图,在Rt△ABC中,∠BAC=90,AB=6,AC=8,点D为边BC的中点,点P为射线AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90.

(1)当DP⊥AB时，求CQ的长；

(2)当BP=2，求CQ的长；

(3)连结AD，若AD平分∠PDQ，求DP：DQ.

Answer 1

【答案】（1）4；（2）CQ的长为或；（3）4:3；

【解析】

（1）首先证明DQ∥AB，根据平行线等分线段定理即可解决问题.

（2）分情况讨论，①中，当点P在线段AB上时，作DM⊥AB,DN⊥AC，由相似推出QN=，推出PM=BM－PB=1，再推出QN=；②中，当点P在AB的延长线上，根据PM,QN的值，CQ=QN+CN计算即可.

（3）首先证明四边形AMDN是正方形，由全等推出PM=NQ，推出PD+DQ的值，再由（2）结论即可计算.

(1)如图1中，

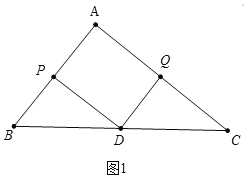
∵DP⊥AB，DQ⊥DP，

∴DQ∥AB，

∵BD=DC，

∴CQ=AQ=4.

(2)①如图2中，当点P在线段AB上时，作DM⊥AB，DN⊥AC，垂足分别为M、N，

则四边形AMDN是矩形，DM、DN分别是△ABC的中位线，DM=4，DN=3，

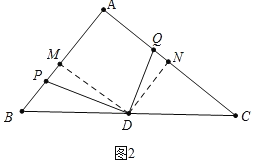
∵∠PDQ=∠MDN=90°，

∴∠PDM=∠QDN,∵∠DNQ∠DMP=90°，

∴△PDM∽△QDN，

∴= =，

∴QN=PM，

∵PM=BMPB=32=1，

∴QN=，

∴CQ=QN+CN=+4=.

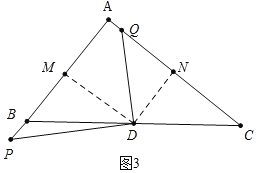
②如图3中,当点P在AB的延长线上时,PM=5,QN=,CQ=QN+CN=4+=，

综上所述,当BP=2,求CQ的长为或.

(3)如图4中，作AM⊥DP于M，AN⊥DQ于N.

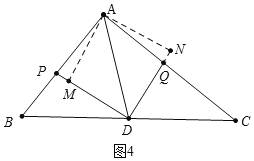
∵AD平分∠PDQ，

∴AM=AN，

∵∠AMD=∠AND=∠MDN=90，

∴四边形AMDN是矩形，∵AM=AN，

∴四边形AMDN是正方形，

∴∠MAN=90，DM=DN，

∵∠BAC=∠MAN=90，

∴∠PAM=∠NAQ，

∴△APM≌△AQN，

∴PM=NQ，

∵AB=6，AC=8，

∴BC= =10，AD=5，

∵PD+DQ=(PM+MD)+(DNQN)=2DM=AD=，

由(2)可知PD:QD=4:3，