题目内容
【题目】一艘观光游船从港口A处以北偏东60°的方向出港观光，航行80海里至C处时发生了侧翻沉船事故，立即发出了求救信号．一艘在港口正东方向B处的海警船接到求救信号，测得事故船在它的北偏东37°方向．
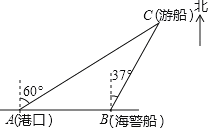
（1）求海警船距离事故船C的距离BC．
（2）若海警船以40海里/小时的速度前往救援，求海警船到达事故船C处大约所需的时间．（温馨提示：sin 53°≈0．8，cos 53°≈0．6）
【答案】（1）50海里，（2）
小时．
【解析】
过点C作CD⊥AB交AB延长线于D．先解Rt△ACD得出CD=
AC=40海里，再解Rt△CBD中，得出BC=
≈50，然后根据时间=路程÷速度即可求出海警船到大事故船C处所需的时间．
如图，过点C作CD⊥AB交AB延长线于D．
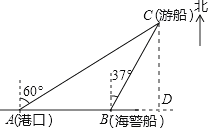
在Rt△ACD中，∵∠ADC=90°，∠CAD=30°，AC=80海里，
∴CD=AC=40海里．
在Rt△CBD中，∵∠CDB=90°，∠CBD=90°-37°=53°，
∴BC=≈
=50（海里），
∴海警船到大事故船C处所需的时间大约为：50÷40=（小时）．
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
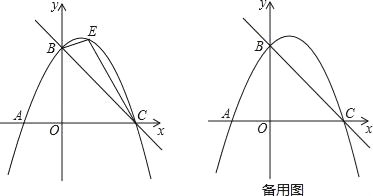
【题目】小东根据学习函数的经验，对函数
的图象与性质进行了探究．下面是小东的探究过程，请补充完整，并解决相关问题：
（1）函数的自变量x的取值范围是 ；
（2）下表是y与x的几组对应值.
x | … |
|
|
| 0 |
| 1 |
| 2 |
| 3 | 4 | … |
y | … |
|
|
| 2 |
| 4 |
| 2 |
|
| m | … |
表中m的值为________________；
（3）如图，在平面直角坐标系中，描出了以上表中各对对应值为坐标的点. 根据描出的点，画出函数的大致图象；
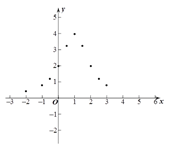
（4）结合函数图象，请写出函数的一条性质：______________________.
（5）解决问题：如果函数与直线y=a的交点有2个，那么a的取值范围是______________ .
