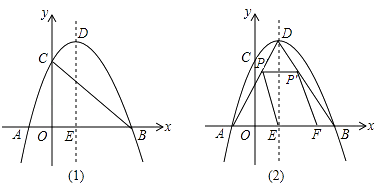题目内容
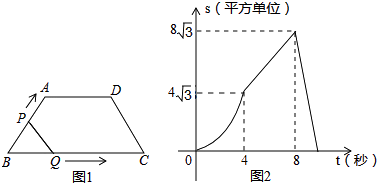
【题目】如图1,在等腰梯形ABCD中,∠B=60°,P、Q同时从B出发,以每秒1个单位长度分别沿B→A→D→C和B→C→D方向运动至相遇时停止.设运动时间为t(秒),△BPQ的面积为S(平方单位),S与t的函数图象如图2,则下列结论错误的是( )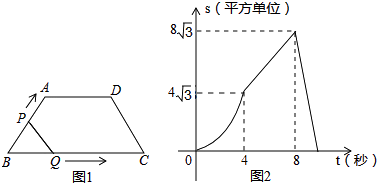
A.当t=4秒时,S=4 ![]()
B.AD=4
C.当4≤t≤8时,S=2 ![]() t
t
D.当t=9秒时,BP平分梯形ABCD的面积
【答案】C
【解析】解:由答图2所示,动点运动过程分为三个阶段: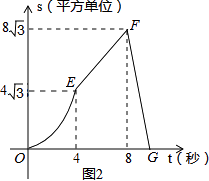
①OE段,函数图象为抛物线,运动图形如答图1﹣1所示.
此时点P在线段AB上、点Q在线段BC上运动.
△BPQ为等边三角形,其边长BP=BQ=t,高h= ![]() t,
t,
∴S= ![]() BQh=
BQh= ![]() t
t ![]() t=
t= ![]() t2 .
t2 .
由函数图象可知,当t=4秒时,S=4 ![]() ,故选项A正确.
,故选项A正确.
②EF段,函数图象为直线,运动图形如答图1﹣2所示.
此时点P在线段AD上、点Q在线段BC上运动.
由函数图象可知,此阶段运动时间为4s,
∴AD=1×4=4,故选项B正确.
设直线EF的解析式为:S=kt+b,将E(4,4 ![]() )、F(8,8
)、F(8,8 ![]() )代入得:
)代入得:![]() ,
,
解得 ![]() ,
,
∴S= ![]() t,故选项C错误.
t,故选项C错误.
③FG段,函数图象为直线,运动图形如答图1﹣3所示.
此时点P、Q均在线段CD上运动.
设梯形高为h,则S梯形ABCD= ![]() (AD+BC)h=
(AD+BC)h= ![]() (4+8)h=6h;
(4+8)h=6h;
当t=9s时,DP=1,则CP=3,
∴S△BCP= ![]() S△BCD=
S△BCD= ![]() ×
× ![]() ×8×h=3h,
×8×h=3h,
∴S△BCP= ![]() S梯形ABCD , 即BP平分梯形ABCD的面积,故选项D正确.
S梯形ABCD , 即BP平分梯形ABCD的面积,故选项D正确.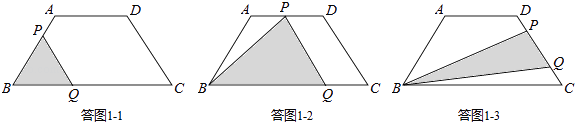
综上所述,错误的结论是C.
故选:C.
【考点精析】认真审题,首先需要了解函数的图象(函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值).