题目内容
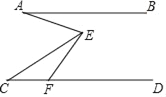
【题目】如图，已知AB∥CD，F为CD上一点，∠EFD=60°，∠AEC=2∠CEF，若6°＜∠BAE＜15°，∠C的度数为整数，则∠C的度数为_____．
【答案】36°或37°．
【解析】分析：先过E作EG∥AB，根据平行线的性质可得∠AEF=∠BAE+∠DFE，再设∠CEF=x，则∠AEC=2x，根据6°＜∠BAE＜15°，即可得到6°＜3x-60°＜15°，解得22°＜x＜25°，进而得到∠C的度数．
详解：如图，过E作EG∥AB，
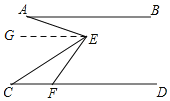
∵AB∥CD，
∴GE∥CD，
∴∠BAE=∠AEG，∠DFE=∠GEF，
∴∠AEF=∠BAE+∠DFE，
设∠CEF=x，则∠AEC=2x，
∴x+2x=∠BAE+60°，
∴∠BAE=3x-60°，
又∵6°＜∠BAE＜15°，
∴6°＜3x-60°＜15°，
解得22°＜x＜25°，
又∵∠DFE是△CEF的外角，∠C的度数为整数，
∴∠C=60°-23°=37°或∠C=60°-24°=36°，
故答案为：36°或37°．
练习册系列答案
相关题目
