题目内容
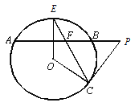
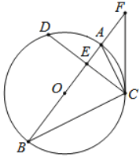
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() 、
、![]() ,点
,点![]() 是
是![]() 延长线上的一点,且
延长线上的一点,且![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1) 连结OC ,根据AB是⊙O的直径得到![]() ,再证明
,再证明![]() ,根据CF经过半径OC的外端得到FC是⊙O的切线;
,根据CF经过半径OC的外端得到FC是⊙O的切线;
(2)先得到∠ACE+∠BAC=90°,根据三角函数得到EC的长度,再根据勾股定理求出圆的半径等于8,再证明△AOC为等边三角形,利用含30°的直角三角形的性质得到FC的长度;
(1)证明:连结OC,
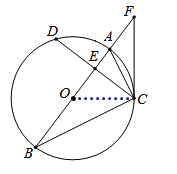
∵AB是⊙O的直径
∴![]()
∵OB=OC
∴∠B=∠OCB
∴![]()
∵∠FCO=∠B
∴![]()
即![]()
又∵CF经过半径OC的外端
∴FC是⊙O的切线.
(2)AB⊥CD
∴![]() ,
,
∴∠ACE+∠BAC=90°,
又在RtABC中,∠B+∠BAC=90°
∴∠ACE=∠B=30°
∴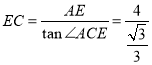
![]() ,
,
设OA=OC=r
即![]() ,
,
解得r=8
∴OE=r-4=8-4=4=AE
又∵CE⊥OA
∴CA=CO=8
∴△AOC为等边三角形,
∴∠FOC=60°,
∴∠F=30°,
在Rt△FOC中,
∵∠OCF=90°,OC=8,∠F=30°,
∴OF=2OC=16
∴![]() ;
;

练习册系列答案
相关题目