题目内容
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD.我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
(1)如图2,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(2)如图3,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则求∠DAB的度数;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,则△DAB的最大面积等于 .
【答案】
(1)
证明:∵∠DAB=60°,AC平分∠DAB,
∴∠DAC=∠CAB=30°,
∴∠D+∠ACD=180°﹣30°=150°,
∵∠BCD=∠ACD+∠ACB=150°,
∴∠D=∠ACB,
∴△ADC∽△ACB.
∴AD:AC=AC:AB,
∴AC2=ABAD,
∴四边形ABCD为“可分四边形”
(2)
解:∵AC平分∠DAB,
∴∠DAC=∠BAC,
∵AC2=ABAD,
∴AD:AC=AC:AB,
∴△ADC∽△ACB,
∴∠D=∠ACB,
∵∠DCB=∠DAB,
∴∠DCB=∠DCA+∠ACB=2∠DAC,
∵∠DAC+∠D+∠ACB=180°,
∴∠DAC+2∠DAC=180°,
解得:∠DAC=60°,
∴∠DAB=120°
(3)8
【解析】(3)∵四边形ABCD为“可分四边形”,AC=4,
∴ABAD=AC2=16,
当DA⊥DB时,△DAB的最大,最大面积为8,
故答案为:8.
(1)由已知得出∠DAC=∠CAB=30°,由三角形内角和定理得出∠D+∠ACD=150°,由∠BCD=∠ACD+∠ACB=150°,得出∠D=∠ACB,证明△ADC∽△ACB.得出对应边成比例,得出AC2=ABAD,即可得出结论;(2)由已知条件可证得△ADC∽△ACB,得出D=∠ACB,再由已知条件和三角形内角和定理得出∠DAC+2∠DAC=180°,求出∠DA=60°,即可得出∠DAB的度数;(3)根据“可分四边形”的定义求出ABAD,计算即可.

【题目】林华在2018年共两次到某商场按照标价购买了A,B两种商品,其购买情况如下表:
购买A商品的数量(个) | 购买B商品的数量(个) | 购买两种商品的总费用(元) | |
第一次购买 | 6 | 5 | 1140 |
第二次购买 | 3 | 7 | 1110 |
(1)分别求出A、B两种商品的标价。
(2)最近商场实行“迎2019新春”的促销活动,A,B两种商品都打折且折扣数相同,于是林华前往商场花1062元又购买了9个A商品和8个B商品,试问本次促销活动中A,B商品的折扣数都为多少?在本次购买中,林华共节约了多少钱?
【题目】问题情景:
如图,在直角坐标系xOy中,点A、B为二次函数y=ax2(a>0)图象上的两点,且点A、B的横坐标分别为m、n(m>n>0),连接OA、AB、OB.设△AOB的面积为S时,解答下列问题: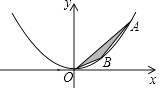
(1)探究:当a=1时,
mn | m﹣n | S | |
m=3,n=1 | 3 | 2 | |
m=5,n=2 | 10 | 3 |
当a=2时,
2mn | m﹣n | S | |
m=3,n=1 | 6 | 2 | |
m=5,n=2 | 20 | 3 |
(2)归纳证明:对任意m、n(m>n>0),猜想S=(用a,m,n表示),并证明你的猜想.
(3)拓展应用:
若点A、B的横坐标分别为m、n(m>0>n),其它条件不变时,△AOB的面积S=(用a,m,n表示).