题目内容
【题目】某地区为了进一步缓解交通拥堵问题,决定修建一条长为6千米的公路.如果平均每天的修建费y(万元)与修建天数x(天)之间在30≤x≤120,具有一次函数的关系,如下表所示.
X | 50 | 60 | 90 | 120 |
y | 40 | 38 | 32 | 26 |
(1)求y关于x的函数解析式;
(2)后来在修建的过程中计划发生改变,政府决定多修2千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了15天,求原计划每天的修建费.
【答案】
(1)解:设y与x之间的函数关系式为y=kx+b(k≠0),由题意,得
![]() ,
,
解得: 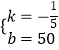 ,
,
∴y与x之间的函数关系式为:y=﹣ ![]() x+50(30≤x≤120)
x+50(30≤x≤120)
(2)解:设原计划要m天完成,则增加2km后用了(m+15)天,由题意,得
![]() ,
,
解得:m=45,
经检验m=45是原方程的根.
∴原计划每天的修建费为:﹣ ![]() ×45+50=41(万元)
×45+50=41(万元)
【解析】(1)设y与x之间的函数关系式为y=kx+b,运用待定系数法就可以求出y与x之间的函数关系式;(2)设原计划要m天完成,则增加2km后用了(m+15)天,根据每天修建的工作量不变建立方程求出其解,就可以求出计划的时间,然后代入(1)的解析式就可以求出结论.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目