题目内容
【题目】阅读下列材料,完成相应任务:
折纸三等分角 |
学习任务:
(1)将剩余部分的证明过程补充完整;
(2)若将图1中的点S与点D重合,重复材料中的操作过程得到图4,请利用图4,直接写出tan15°=(不必化简)
【答案】
(1)解:剩余的证明过程如下:
∵ME=PQ,EB=QT,ME=EB,
∴PQ=QT,
∴BP=BT,
∴∠PBQ=∠TBQ,
∵TK=BE,
∴TK=TQ,
∴∠QBT=∠TBC,
∴射线BQ,BT是∠SBC的三等分线
(2)2﹣ ![]()
【解析】解:(2)同(1)可知:射线BQ,BT是∠DBC的三等分线,
过T作TJ⊥BC,垂足为J,如图所示:
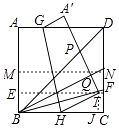
则∠TBJ= ![]() ∠DBC,
∠DBC,
∵四边形ABCD为正方形,
∴∠DBC=45°,
∴∠TBJ=15°,
由折叠性质得:BH=HT,
∴∠TBJ=∠HTB=15°,
∴∠THJ=30°,
设BC=4,则BE=1,
∵将正方形ABCD对折,折痕为记为MN,再将矩形MBCN对折,折痕记为EF,TJ⊥BC,
∴四边形EBJT为矩形,
∴TJ=BE=1,
在Rt△THJ中,∠THJ=30°,
∴HT=2TJ=2,HJ=cot30°TJ= ![]() ×1=
×1= ![]() ,
,
∴BJ=BH+HJ=HT+HJ=2+ ![]() ,tan∠TBJ=
,tan∠TBJ= ![]() =
= ![]() =2﹣
=2﹣ ![]() ,
,
即tan15°=2﹣ ![]() ;
;
所以答案是:2﹣ ![]() .
.
【考点精析】掌握翻折变换(折叠问题)和锐角三角函数的定义是解答本题的根本,需要知道折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案【题目】下表是橘子的销售额随橘子卖出质量的变化表:
质量/千克 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
销售额/元 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | … |
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当橘子卖出5千克时,销售额是_______元.
(3)如果用![]() 表示橘子卖出的质量,
表示橘子卖出的质量,![]() 表示销售额,按表中给出的关系,
表示销售额,按表中给出的关系,![]() 与
与![]() 之间的关系式为______.
之间的关系式为______.
(4)当橘子的销售额是100元时,共卖出多少千克橘子?