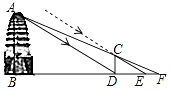
[题目]已知:如图.△ABC中.∠BAD=∠EBC.AD交BE于F．(1)试说明:∠BFD=∠ABC,(2)若∠ABC=40°.EG∥AD.EH⊥BE.求∠HEG的度数．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知：如图，△ABC中，∠BAD=∠EBC，AD交BE于F．

（1）试说明：∠BFD=∠ABC；

（2）若∠ABC=40°，EG∥AD，EH⊥BE，求∠HEG的度数．

【答案】（1）见解析；（2）∠HEG=50°．

【解析】

（1）根据三角形的外角性质即可得出结论；
（2）根据三角形内角和和互余进行分析解答即可．

（1）∵∠BFD是△ABF的外角

∴∠BFD=∠BAD+∠ABF

∵∠BAD=∠EBC

∴∠BAD+∠ABF=∠EBC+∠ABF

即∠BFD=∠ABC

（2）∵∠ABC=40°，∠BFD=∠ABC

∴∠BFD=40°

∵EG∥AD

∴∠BFD=∠BEG

∴∠BEG=40°

∵EH⊥BE

∴∠BEH=90°

∴∠HEG=∠BEH-∠BEG=50°

练习册系列答案

相关题目

【题目】如图，在中，，，，为边上一动点，于，于，为中点，则的最小值为（）

A.B.4C.5D.

【题目】如图是位于陕西省西安市荐福寺内的小雁塔，是中国早期方形密檐式砖塔的典型作品，并作为丝绸之路的一处重要遗址点，被列入《世界遗产名录》．小铭、小希等几位同学想利用一些测量工具和所学的几何知识测量小雁塔的高度，由于观测点与小雁塔底部间的距离不易测量，因此经过研究需要进行两次测量，于是在阳光下，他们首先利用影长进行测量，方法如下：小铭在小雁塔的影子顶端D处竖直立一根木棒CD，并测得此时木棒的影长DE=2.4米；然后，小希在BD的延长线上找出一点F，使得A、C、F三点在同一直线上，并测得DF=2.5米．已知图中所有点均在同一平面内，木棒高CD=1.72米，AB⊥BF，CD⊥BF，试根据以上测量数据，求小雁塔的高度AB．

【题目】问题探究：探究与应用
（1）如图1，在正方形ABCD中，AB=2，点E是边AD的中点，请在对角线AC上找一点P，使得PE+PD的值最小，并求出这个最小值；（不用写作法，保留作图痕迹）

（2）如图2，在矩形ABCD中，AB=6，BC=8，点E是边BC的中点，若点P是边AB上一动点，当△PED的周长最小时，求BP的长度；
问题解决：

（3）某市规划在市中心广场内修建一个矩形的活动中心，如图3，矩形OABC是它的规划图纸，其中A为入口，已知OA=30，OC=20，点E是边AB的中点，以顶点O为原点，OA所在的直线为x轴，OC所在的直线为y轴，建立平面直角坐标系，点D是边OA上一点，若将△ABD沿BD翻折，点A恰好落在边BC上的点F处，在点F处设一出口，点M、N分别是边OA、OC上的点，现规划在点M、N、F、E四处各安置一个健身器材，并依次修建MN、NF、FE及EM四条小路，则是否存在点M、N，使得这四条小路的总长度最小？若存在，求出这个最小值；若不存在，请说明理由．

【题目】如图，点A是反比例函数y= （x＞0）的图象上一点，OA与反比例函数y= （x＞0）的图象交于点C，点B在y轴的正半轴上，且AB=OA，若△ABC的面积为6，则k的值为．

【题目】若x满足，求的值．

解：设，，则，，

所以== ==32-2×2=5．

请运用上面的方法求解下面的问题：

（1）若满足，求的值；

（2）已知正方形ABCD的边长为，E、F分别是AD、DC上的点，且AE=1，CF=3，长方形EMFD的面积是35，求长方形EMFD的周长．

【题目】阅读下列材料，完成相应任务：

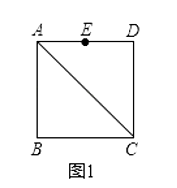
折纸三等分角
三等分角问题（trisection of an angle）是二千四百年前，古希腊人提出的几何三大作图问题之一（三等分任意角、化圆为方、倍立方），即用圆规与直尺（没有刻度，只能做直线的尺子）把一任意角三等分，这问题曾吸引着许多人去研究，但无一成功．1837年法国数学家凡齐尔（1814～1848）运用代数方法证明了，仅用尺规不可鞥呢三等分角．
如果作图工具没有限制，将条件放宽，将任意角三等分是可以解决的．下面介绍一种折纸三等分任意锐角的方法：
①在正方形纸片上折出任意∠SBC，将正方形ABCD对折，折痕为记为MN，再将矩形MBCN对折，折痕记为EF，得到图1；
②翻折左下角使点B与EF上的点T重合，点M与SB上的点P重合，点E对折后的对应点记为Q，折痕为记为GH，得到图2；
③折出射线BQ，BT，得到图3，则射线BQ，BT就是∠SBC的三等分线．

下面是证明BQ，BT是∠SBC三等分线的部分过程：
证明：过T作TK⊥BC，垂足为K，则四边形EBKT为矩形
根据折叠，得EB=QT，∠EBT=∠QTB，BT=TB
∴△EBT≌△QTB，
∴∠BQT=∠TEB=90°，
∴BQ⊥PT
…

学习任务：
（1）将剩余部分的证明过程补充完整；
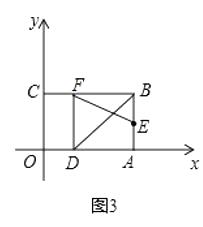
（2）若将图1中的点S与点D重合，重复材料中的操作过程得到图4，请利用图4，直接写出tan15°=（不必化简）

【题目】如图，正方形ABCD的边长为，连接AC，AE平分∠CAD，交BC的延长线于点E，FA⊥AE，交CB的延长线于点F，则EF的长为（）

A.2
B.4
C.2
D.4

【题目】为了保护环境，某化工厂一期工程完成后购买了台甲型和台乙型污水处理设备，共花费资金万元，且每台乙型设备的价格是每台甲型设备价格的，实际运行中发现，每台甲型设备每月能处理污水吨，每台乙型设备每月能处理污水吨．今年该厂二期工程即将完成产生的污水将大大增加，于是该厂决定再购买甲、乙两种型号设备共台用于二期工程的污水处理，预算本次购买资金不超过万元，预计二期工程完成后每月将产生不少于吨污水．

试题分类