题目内容
【题目】已知两个分别含有30°,45°角的一副直角三角板.
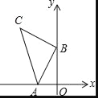
(1)如图1叠放在一起
若OC恰好平分∠AOB,则∠AOD= 度;
若∠AOC=40°,则∠BOD= 度;
(2)如图2叠放在一起,∠AOD=4∠BOC,试计算∠AOC的度数.

【答案】(1)135,40;(2)∠AOC的度数为110°.
【解析】
(1)①根据角平分线的定义求出∠AOC,再根据∠AOD=∠AOC+∠COD代入数据进行计算即可得解;
②由已知可求得∠BOC,再根据∠BOD=∠COD-∠BOC代入数据进行计算即可得解;
(2)由已知可求得∠BOD,再根据∠AOC=∠AOB+∠COD-∠BOD代入数据进行计算即可得解.
(1)①∵OC平分∠AOB,∠AOB=90°,
∴∠AOC=![]() ∠AOB=45°,
∠AOB=45°,
∴∠AOD=∠AOC+∠COD=45°+90°=135°;
②由已知∠BOC=90°-∠40°=50°,
∴∠BOD=∠COD-∠BOC=90°-50°=40°,
故答案为:135,40
(2)∵∠AOD=4∠BOC,
∴∠AOB-∠BOD=4(∠COD-∠BOD),
即90°-∠BOD=4(-30°∠BOD),解得:∠BOD=10°,
∴∠AOC=∠AOB+∠COD-∠BOD=90°+30°-10°=110°
即∠AOC的度数为110°.

练习册系列答案
相关题目