Question

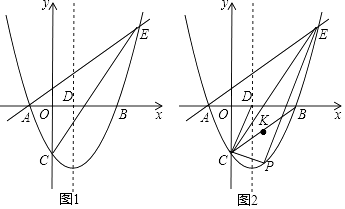
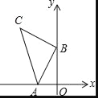
【题目】如图，在平面直角坐标系中，点A的坐标为（﹣2，0），点B的坐标为（0，n），以点B为直角顶点，点C在第二象限内，作等腰直角△ABC．则点C的坐标是_____（用字母n表示）．

Answer 1

【答案】（﹣n，2+n）．

【解析】

作CE⊥y轴于E，如图1，根据题意通过“角角边”证明△CBE≌△BAO，得到CE=BO=n，BE=AO=2，然后根据C点所在象限即可得到答案.

（1）作CE⊥y轴于E，如图1，

∵A（﹣2，0），B（0，n），

∴OA=2，OB=n，

∵△ABC为等腰直角三角形，

∴∠CEB=∠AOB=∠CBA=90°，BC=AB，

∴∠ECB+∠EBC=90°，∠CBE+∠ABO=90°，

∴∠ECB=∠ABO，

在△CBE和△BAO中

，

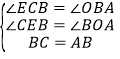∴△CBE≌△BAO（AAS），

∴CE=BO=n，BE=AO=2，

即OE=2+n，

∴C（﹣n，2+n）．

故答案为：（﹣n，2+n）．