题目内容
【题目】在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE= 度;
(2)设∠BAC= ![]() ,∠DCE=
,∠DCE= ![]() .
.
① 如图2,当点D在线段CB上,∠BAC≠90°时,请你探究![]() 与
与![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
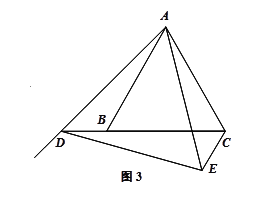
② 如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时![]() 与
与![]() 之间的数量关系(不需证明).
之间的数量关系(不需证明).

【答案】(1) 90 ;(2)①![]() , 理由见解析;②图形见解析,
, 理由见解析;②图形见解析, ![]()
【解析】试题分析:(1)利用等腰三角形证明![]() ABD
ABD![]() ACE,所以∠ECA=∠DBA,所以∠DCE=90°.(2)方法类似(1)证明△ABD≌△ACE,所以∠B=∠ACE,再利用角的关系求
ACE,所以∠ECA=∠DBA,所以∠DCE=90°.(2)方法类似(1)证明△ABD≌△ACE,所以∠B=∠ACE,再利用角的关系求![]() . (3)同理方法类似(1).
. (3)同理方法类似(1).
试题解析:
解:(1) 90 度.
∠DAE=∠BAC ,所以∠BAD=∠EAC,AB=AC,AD=AE,所以![]() ABD
ABD![]() ACE,所以∠ECA=∠DBA,所以∠ECA=90°.
ACE,所以∠ECA=∠DBA,所以∠ECA=90°.
(2)①![]() .
.
理由:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE,
又AB=AC,AD=AE,
∴△ABD≌△ACE,
∴∠B=∠ACE.∴∠B+∠ACB=∠ACE+∠ACB,
∴![]() .∵
.∵![]() ,
,
∴![]() .
.
(3)补充图形如下, ![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】一股民上星期五买进某公司股票![]() 股,每股
股,每股![]() 元,下表为本周内每日该股票的涨跌情况(单位:元)
元,下表为本周内每日该股票的涨跌情况(单位:元)
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 |
|
|
|
|
|
![]() 星期三收盘时,每股是________元;
星期三收盘时,每股是________元;
![]() 本周内每股最高价为________元,每股最低价为________元;
本周内每股最高价为________元,每股最低价为________元;
![]() 已知该股民买进股票时付了
已知该股民买进股票时付了![]() ‰的手续费,卖出时还需付成交额
‰的手续费,卖出时还需付成交额![]() ‰的手续费和
‰的手续费和![]() ‰的交易锐,如果该股民在星期五收盘前将全部股票卖出,他的收益情况如何?
‰的交易锐,如果该股民在星期五收盘前将全部股票卖出,他的收益情况如何?