题目内容
已知:如图1,矩形ABCD中,AB=6,BC=8,E、F、G、H分别是AB、BC、CD、DA四条边上的点(且不与各边顶点重合),设m=EF+FG+GH+HE,探索m的取值范围.
(1)如图2,当E、F、G、H分别是AB、BC、CD、DA四边中点时,m= .
(2)为了解决这个问题,小贝同学采用轴对称的方法,如图3,将整个图形以CD为对称轴
翻折,接着再连续翻折两次,从而找到解决问题的途径,求得m的取值范围.①请在图3
中补全小贝同学翻折后的图形;②请你根据①中的图形,求出m的取值范围,并简要说明理
由.
(1)如图2,当E、F、G、H分别是AB、BC、CD、DA四边中点时,m= .
(2)为了解决这个问题,小贝同学采用轴对称的方法,如图3,将整个图形以CD为对称轴
翻折,接着再连续翻折两次,从而找到解决问题的途径,求得m的取值范围.①请在图3
中补全小贝同学翻折后的图形;②请你根据①中的图形,求出m的取值范围,并简要说明理
由.

(1)20;
(2)如图所示(虚线可以不画),
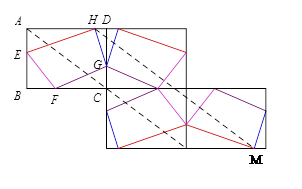
由图形可知,四边形的周长即折线HM的长,由两点之间线段最短可知,折线HM≥HM,即周长不小于20;
又由题可知,四边形周长小于矩形ABCD的周长,即周长小于28,
∴ 20≤m<28.
(2)如图所示(虚线可以不画),

由图形可知,四边形的周长即折线HM的长,由两点之间线段最短可知,折线HM≥HM,即周长不小于20;
又由题可知,四边形周长小于矩形ABCD的周长,即周长小于28,
∴ 20≤m<28.
(1)根据勾股定理求出EF、FG、GH、HE的值,然后得出m的值;
(2)利用轴对称的性质进行讨论。
(2)利用轴对称的性质进行讨论。

练习册系列答案
相关题目
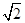 时,求CM的长.
时,求CM的长.


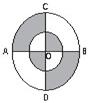
 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转 得到点
得到点 的坐标为___________。
的坐标为___________。

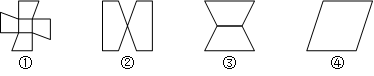
 、
、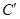 。
。 ;
;