题目内容
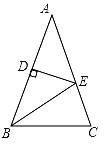
【题目】如图，已知AB=AC，∠A=36°，AB的中垂线交AC于点E，交AB于点D，下面4个结论：
①射线BE是∠ABC的平分线；②△BCE是等腰三角形；③△ABE是等腰三角形；④△ADE≌△BDE；
（1）判断其中正确的结论是哪几个？
（2）从你认为是正确的结论中选一个加以说明．
【答案】(1) ①②③④;（2）证明见解析.
【解析】试题分析：(1)利用垂直平分线到两端点距离相等，证明③正确，再证明④中三角形全等，利用等腰三角形底角相等，说明∠ABE=∠CBE, ①正确,所以②△BCE是等腰三角形.①②③④均正确.(2)同（1）
试题解析：
(1) AB的中垂线交AC于点E，
AE=BE,
△ABE是等腰三角形, ③正确.
AD=AD,AE=BE,∠ADE=∠BDE,
△ADE≌△BDE,④正确.
AB=AC，∠A=36°，
∠C=72°.∠EBC=36°，
射线BE是∠ABC的平分线①正确.
∠BEC=72°.
△BCE是等腰三角形，②正确.
①②③④都正确.
(2)证明见（1）详解.
练习册系列答案
智慧小复习系列答案
相关题目
