��Ŀ����
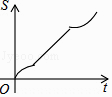
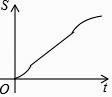
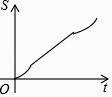
����Ŀ����ˮ��ԭ��ˮ���¶�Ϊ20�棬ͨ�翪������ˮ���Զ���ʼ���ȣ��˹�����ˮ��y�뿪��ʱ��x����һ�κ�����ϵ���������ȵ�100�����Զ�ֹͣ���ȣ����ˮ�¿�ʼ�½����˹���ˮ��y�뿪��ʱ��x�ɷ�������ϵ������ˮ�½���20��ʱ����ˮ�����Զ���ʼ���ȣ����ظ�����������ͼ��ʾ��������ͼ���ṩ����Ϣ������������⣺
��1����0��x��8����ˮ��y�뿪��ʱ��x�ĺ�����ϵ.
��2����ͼ��t��ֵ.
��3����ͨ���45������ˮ����ˮ��ԼΪ���ٶȣ���ͨ���60������ˮ����ˮ��ԼΪ���ٶȣ�

���𰸡���1����������ʽΪ��y=10x+20�� ��2��t=40�� ��3��45����ʱ����ˮ���ڵ��¶�ԼΪ70����60����ʱ����ˮ���ڵ��¶�ԼΪ40��.
��������������
��1���������Ϻ���ͼ������������ϵʽΪy=kx+b�����㣨0��20���͵㣨8��100���������躯����ϵʽ�г������飬�ⷽ�������k��b��ֵ���ɵõ���������ϵʽ��
��2����ˮ���½�������y��x��ĺ�����ϵʽΪ��![]() �����㣨8��100�����������ϵʽ���m��ֵ�����ɵõ�ˮ���½�������y��x��ĺ�����ϵʽΪ
�����㣨8��100�����������ϵʽ���m��ֵ�����ɵõ�ˮ���½�������y��x��ĺ�����ϵʽΪ![]() ���ٽ�y=20�������ú�����ϵʽ�������t=40��
���ٽ�y=20�������ú�����ϵʽ�������t=40��
��3������x=45ʱ����45-t=5<8��֪����ʱ���ڼ��ȽΣ���x=5���루1�������ú�����ϵʽ������ô�ʱ��Ӧ��ˮ�£�����x=60ʱ����60-40=20>8����20<40��֪����ʱ����ˮ���½�������x=20���루2�������ú�����ϵʽ������ô�ʱ��Ӧ��ˮ����.
�����
��1����0��x��8ʱ����ˮ��y���棩�뿪��ʱ��x���֣��ĺ�����ϵΪ��y=kx+b��
�������⣬��![]() ����ã�
����ã�![]() ��
��
������������ʽΪ��y=10x+20��
��2����ˮ���½������У���ˮ��y���棩��
����ʱ��x���֣��ĺ�����ϵʽΪ��![]() ��
��
�������⣬�ã�100=![]() ����m=800����
����m=800����![]() ��
��
��y=20ʱ��20=![]() ����ã�t=40��
����ã�t=40��
��3������45��40=5��8��
��45����ʱ�����ڼ��ȽΣ�
�ߵ�x=5ʱ��y=10��5+20=70��
��45����ʱ����ˮ���ڵ��¶�ԼΪ70����
�ڡ�60��40=20>8����20<40��
��60����ʱ������ˮ���½��Σ�
�ߵ�x=20ʱ��y=![]() ��
��
��60����ʱ����ˮ���ڵ��¶�ԼΪ40��.