题目内容
【题目】如图,正六边形ABCDEF的边长为6cm,P是对角线BE上一动点,过点P作直线l与BE垂直,动点P从B点出发且以1cm/s的速度匀速平移至E点.设直线l扫过正六边形ABCDEF区域的面积为S(cm2),点P的运动时间为t(s),下列能反映S与t之间函数关系的大致图象是( )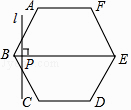
A.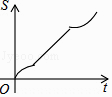
B.
C.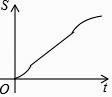
D.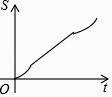
【答案】C
【解析】解:由题意得:BP=t,
如图1,连接AC,交BE于G,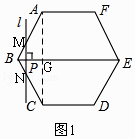
Rt△ABG中,AB=6,∠ABG=60°,
∴∠BAG=30°,
∴BG= ![]() AB=3,
AB=3,
由勾股定理得:AG= ![]() =3
=3 ![]() ,
,
∴AC=2AG=6 ![]() ,
,
当0≤t≤3时,PM= ![]() t,
t,
∴MN=2 ![]() t,
t,
S=S△BMN= ![]() MNPB=
MNPB= ![]() =
= ![]() ,
,
所以选项A和B不正确;
如图2,当9≤t≤12时,PE=12﹣t,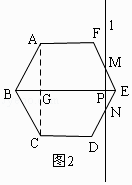
∵∠MEP=60°,
∴tan∠MEP= ![]() ,
,
∴PM= ![]() (12﹣t),
(12﹣t),
∴MN=2PM=2 ![]() (12﹣t),
(12﹣t),
∴S=S正六边形﹣S△EMN ,
=2× ![]() (AF+BE)×AG﹣
(AF+BE)×AG﹣ ![]() MNPE,
MNPE,
=(6+12)×3 ![]() ﹣
﹣ ![]() ×
× ![]() (12﹣t)(12﹣t),
(12﹣t)(12﹣t),
=54 ![]() ﹣
﹣ ![]() (144﹣24t+t2),
(144﹣24t+t2),
=﹣ ![]() +24
+24 ![]() t﹣90
t﹣90 ![]() ,
,
此二次函数的开口向下,
所以选项C正确,选项D不正确;
故选C.
从给出的图象中看,中间位置的图象一致,只要计算两边取值中的图象即可作出判断;先计算点P从B到G时扫过的面积S,发现是二次函数,且开口向下,可以否定和B,再计算点P从9≤t≤12时扫过的面积为正六边形的面积﹣△EMN的面积,计算得到一个开口向下的二次函数,由此作判断.

【题目】某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图. 上网查找学习资源方式频数分布表
查找方式 | 频数 | 频率 |
搜索引擎 | 16 | 32% |
专题网站 | 15 | a |
在线网校 | 4 | 8% |
试题题库 | 10 | 20% |
其他 | b | 10% |
(1)频数分布表中a,b的值:a=;b=;
(2)补全频数分布直方图; 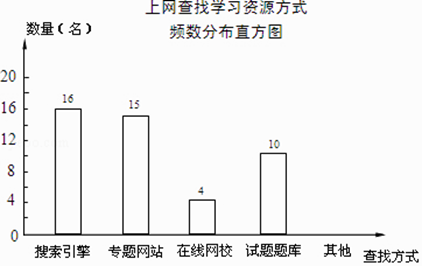
(3)若全校有1000名学生,估计该校利用搜索引擎上网查找学习资源的学生有多少名?
【题目】我国古籍《周髀算经》中早有记载“勾三股四弦五”,下面我们来探究两类特殊的勾股数.通过观察完成下面两个表格中的空格(以下a、b、c为Rt△ABC的三边,且a<b<c):
表一 表二
a | b | c | a | b | c | |
3 | 4 | 5 | 6 | 8 | 10 | |
5 | 12 | 13 | 8 | 15 | 17 | |
7 | 24 | 25 | 10 | 24 | 26 | |
9 | 41 | 12 | 37 |
(1)仔细观察,表一中a为大于1的奇数,此时b、c的数量关系是_____________,
a、b、c之间的数量关系是_________________________;
(2)仔细观察,表二中a为大于4的偶数,此时b、c的数量关系是_____________,
a、b、c之间的数量关系是_________________________;
(3)我们还发现,表一中的三边长“3,4,5”与表二中的“6,8,10”成倍数关系,表一中的“5,12,13”与表二中的“10,24,26”恰好也成倍数关系……请直接利用这一规律计算:在Rt△ABC中,当![]() ,
,![]() 时,斜边c的值.
时,斜边c的值.