题目内容
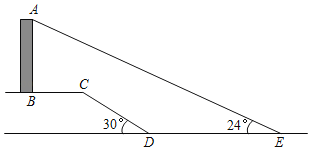
【题目】如图，要测量一垂直于水平面的建筑物AB的高度，小明从建筑物底端B出发，沿水平方向向右走30米到达点C，又经过一段坡角为30°，长为20米的斜坡CD，然后再沿水平方向向右走了50米到达点E(A，B，C，D，E均在同一平面内)．在E处测得建筑物顶端A的仰角为24°，求建筑物AB的高度．(结果保留根号，参考数据：sin24°≈
，cos24°≈
，tan24°＝
)
【答案】筑物AB的高度是
米．
【解析】
作BM⊥ED交ED的延长线于M，CN⊥DM于N．首先解直角三角形Rt△CDN，求出CN，DN，再根据
，构建方程即可解决问题．
解：作BM⊥ED交ED的延长线于M，CN⊥DM于N．
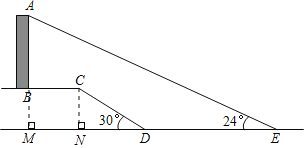
在Rt△CDN中，∵∠CDN＝30°，CD＝20米，
∴CN＝CDsin30°＝10米，DN＝CDcos30°＝5
米，
∵四边形BMNC是矩形，
∴BM＝CN＝10米，BC＝MN＝30米，EM＝MN+DN+DE＝(80+5)米，
在
中，，
，
．
答：建筑物AB的高度是米．
练习册系列答案
相关题目
