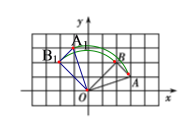
[题目]已知△OAB在平面直角坐标系中的位置如图所示.将△ABO绕原点O逆时针旋转90°得到△OA1B1．(1)画出△OA1B1.并写出点A1.B1的坐标,(2)求△ABO绕原点O逆时针旋转90°扫过的面积．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知△OAB在平面直角坐标系中的位置如图所示，将△ABO绕原点O逆时针旋转90°得到△OA1B1．

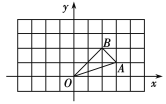
（1）画出△OA1B1，并写出点A1、B1的坐标；

（2）求△ABO绕原点O逆时针旋转90°扫过的面积．

【答案】(1) 作图见解析；A1（-1，3） B1（-2，2）；(2) ．

【解析】

（1）先画出点A，B的对应点A1，B1，再顺次连接起来，即可；

（2）由题意得：△ABO绕原点O逆时针旋转90°扫过的面积=，进而即可求解．

（1）△OA1B1如图所示，根据△OA1B1在坐标系中的位置，得A1(-1，3)， B1(-2，2)；

（2）由题意得：AB=，OB=，OA=，

∵，

∴△ABO是直角三角形，

∴△ABO绕原点O逆时针旋转90°扫过的面积=

=．

练习册系列答案

现代文阅读系列答案

木头马现代文阅读系列答案

开心语文现代文阅读技能训练100篇系列答案

（1）求每部A型手机和B型手机的销售利润分别为多少元？

（2）该商店计划一次购进两种型号的手机共110部，其中A型手机的进货量不超过B型手机的2倍．设购进B型手机n部，这110部手机的销售总利润为y元．

①求y关于n的函数关系式；

②该手机店购进A型、B型手机各多少部，才能使销售总利润最大？

（3）实际进货时，厂家对B型手机出厂价下调m（30＜m＜100）元，且限定商店最多购进B型手机80台．若商店保持两种手机的售价不变，请你根据以上信息及（2）中的条件，设计出使这110部手机销售总利润最大的进货方案．

【题目】为了创建文明城市，增强学生的环保意识．随机抽取8名学生，对他们的垃圾分类投放情况进行调查，这8名学生分别标记为，其中“√”表示投放正确，“×”表示投放错误，统计情况如下表．

学生垃圾类别
厨余垃圾	√	√	√	√	√	√	√	√
可回收垃圾	√	×	√	×	×	√	√	√
有害垃圾	×	√	×	√	√	×	×	√
其他垃圾	×	√	√	×	×	√	√	√

（1）求8名学生中至少有三类垃圾投放正确的概率；

（2）为进一步了解垃圾分类投放情况，现从8名学生里“有害垃圾”投放错误的学生中随机抽取两人接受采访，试用标记的字母列举所有可能抽取的结果．

【题目】如图，在△ABC中，tan∠BACtan∠ABC=1，⊙O经过A、B两点，分别交AC、BC于D、E两点，若DE=10，AB=24，则⊙O的半径为（）

A.B.

C.13D.

【题目】如图，在等边△ABC中，点D、E分别在边AB、BC上，AD=BE，CD与AE交于F．

（1）求∠AFD的度数；

（2）若BE=m，CE=n．

①求的值；（用含有m和n的式子表示）

②若=，直接写出的值．

【题目】某市精准扶贫工作已经进入攻坚阶段，贫困的张大爷在某单位的帮扶下，把一片坡地改造后种植了大樱桃.今年正式上市销售，在销售30天中，第一天卖出20千克，为了扩大销量，在一段时间内采取降价措施，每天比前一天多卖出4千克．当售价不变时，销售量也不发生变化．已知种植销售大樱桃的成本为18元／千克，设第天的销售价元／千克，与函数关系如下表：

表一

天数	1	2	3	……	……	20
售价（元／千克）	37.5	37	36.5	……	……	28

表二

天数	21	22	……	……	30
售价（元／千克）	28	28	……	……	28

（1）求与函数解析式；

（2）求销售大樱桃第几天时，当天的利润最大？最大利润是多少？

（3）销售大樱桃的30天中，当天利润不低于元的共有多少天？

【题目】如图，要测量一垂直于水平面的建筑物AB的高度，小明从建筑物底端B出发，沿水平方向向右走30米到达点C，又经过一段坡角为30°，长为20米的斜坡CD，然后再沿水平方向向右走了50米到达点E(A，B，C，D，E均在同一平面内)．在E处测得建筑物顶端A的仰角为24°，求建筑物AB的高度．(结果保留根号，参考数据：sin24°≈，cos24°≈，tan24°＝)