题目内容
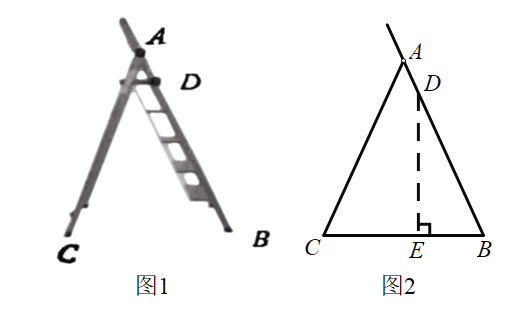
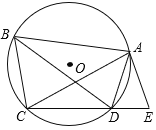
【题目】如图,四边形ABCD内接于⊙O,已知AB=AC,延长CD至点E,使CE=BD,连结AE.
(1)求证:AD平分∠BDE;
(2)若AB∥CD,求证:AE是⊙O的切线.
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)根据等腰三角形的性质和圆内接四边形的性质得到∠ADE=∠ADB,根据角平分线的定义即可得到结论;
(2)根据平行线的性质得到∠ADE=∠DAB,求得∠BAD=∠ADB,根据垂径定理得到AT⊥BC,根据平行四边形的性质得到AE∥BC,于是得到结论.
(1)证明:∵四边形ABCD内接于⊙O
∴∠ABC+∠ADC=180°
∴∠ABC=∠ADE
∵AB=AC
∴∠ABC=∠ACB
∵∠ACB=∠ADB
∴∠ADB=∠ADE
∴AD平分∠BDE
(2)解: AB∥CD,
∴∠ADE=∠DAB,
∵∠ADB=∠ADE,
∴∠BAD=∠ADB,
∴AB=BD
∵CE=BD,
∴AB=CE
∵AC=AB,
![]()

连接OA并延长交BC于T
∴AT⊥BC,
∵AB∥CE,AB=CE
∴四边形ABCE是平行四边形,
∴AE∥BC,
∴AT⊥AE,
∴AE是⊙O的切线.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
【题目】某水果店计划购进甲、乙两种高档水果共400千克,每千克的售价、成本与购进数量(千克)之间关系如表:
每千克售价(元) | 每千克成本(元) | |
甲 | ﹣0.1x+100 | 50 |
乙 | ﹣0.2x+120(0<x≤200) | 60 |
|
(1)若甲、乙两种水果全部售完,求水果店获得总利润y(元)与购进乙种水果x(千克)之间的函数关系式(其他成本不计);
(2)若购进两种水果都不少于100千克,当两种水果全部售完,水果能获得的最大利润.