题目内容
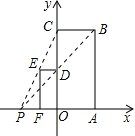
【题目】如图，已知矩形OABC与矩形ODEF是位似图形，P是位似中心，若点B的坐标为
，点E的坐标为
，则点P的坐标为______．
【答案】
【解析】分析：由矩形OABC中，点B的坐标为（2，4），可求得点C的坐标，又由矩形OABC与矩形ODEF是位似图形，P是位似中心，点C的对应点点E的坐标为（-1，2），即可求得其位似比，继而求得答案．
详解：∵四边形OABC是矩形，点B的坐标为（2，4）， ∴OC=AB=4，OA=2，
∴点C的坐标为：（0，4），
∵矩形OABC与矩形ODEF是位似图形，P是位似中心，点E的坐标为（-1，2），
∴位似比为：2， ∴OP：AP=OD：AB=1：2， 设OP=x，则
， 解得：x=2，
∴OP=2， 即点P的坐标为：（-2，0）．
练习册系列答案
相关题目
【题目】某同学在用描点法画二次函数
的图象时，列出下面的表格：
x |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
根据表格提供的信息，有下列结论：
该抛物线的对称轴是直线
；
；
该抛物线与y轴的交点坐标为
；
若点
是该抛物线上一点，则
其中错误的个数是
A. 4 B. 3 C. 2 D. 1
