题目内容
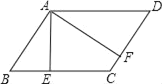
【题目】如图，在ABCD中，AE⊥BC于点E，AF⊥CD于点F，若AE＝4，AF＝6，且ABCD的周长为40，则ABCD的面积为（ ）
A. 24B. 36C. 40D. 48
【答案】D
【解析】
首先根据平行四边形的性质可得AB=CD，AD=BC，可得，再利用其面积的求法S=BC×AE=CD×AF，可得4AE=6CD，列出方程组，求出平行四边形的各边长，再求其面积
设BC=x，CD=y
∵四边形ABCD是平行四边形，
∴AB=CD，AD=BC，
∵ABCD的周长为40，
∴x+y=20，
∵∠B=∠D,∠AEB=∠AFD=90°，
∴△ABE∽△ADF，
∴
=
=
=
∵AE=4，AF=6，
∴4x=6y，
得方程组：
解得：
∴S平行四边形ABCD=BC×AE=12×4=48.
故答案为：48.
练习册系列答案
相关题目
【题目】某同学在用描点法画二次函数
的图象时，列出下面的表格：
x |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
根据表格提供的信息，有下列结论：
该抛物线的对称轴是直线
；
；
该抛物线与y轴的交点坐标为
；
若点
是该抛物线上一点，则
其中错误的个数是
A. 4 B. 3 C. 2 D. 1
