Question

【题目】已知Rt△ABC中，AC=5，BC=12，∠ACB=90°，P是AB边上的动点（与点A、B不重合），Q是BC边上的动点（与点B、C不重合）

（1）如图，当PQ∥AC，且Q为BC的中点时，求线段CP的长；

（2）当PQ与AC不平行时，△CPQ可能为直角三角形吗？若有可能，请求出线段CQ的长的取值范围；若不可能，请说明理由．

Answer 1

【答案】（1）；（2）详见解析.

【解析】试题分析：

（1）由题意易得AB=13，由Q是BC中点，PQ∥AC可得点P是AB中点，从而可得CP=AB=；

（2）当AC与PQ不平行时，只有∠CPQ为直角，△CPQ才可能是直角三角形．根据圆中，直径所对的圆周角是直角，以CQ为直径作半圆D，当半圆D和直线AB有公共点时，点P运动到公共点处，∠PCQ就是直角；由此以CQ为直径作半圆D，当半圆D与AB相切时，设切点为M，连接DM，则DM⊥AB，设CD=x，则CQ=2x，DM=x，DB=12﹣x；在Rt△DMB中，由DB2=DM2+MB2，结合已知条件建立关于x的方程即可解得x的值，从而可得对应的CQ的值，再结合只有当半圆D与直线AB有公共点时，∠PCQ才有可能是直角即可求得CQ的取值范围.

试题解析：

（1）在Rt△ABC中∠ACB=90°，AC=5，BC=12，

∴AB=13；

∵Q是BC的中点，

∴CQ=QB；

又∵PQ∥AC，

∴AP=PB，即P是AB的中点，

∴Rt△ABC中，CP=．

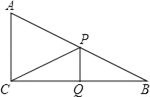
（2）当AC与PQ不平行时，只有∠CPQ为直角，△CPQ才可能是直角三角形．

以CQ为直径作半圆D，当半圆D与AB相切时，设切点为M，连接DM，则

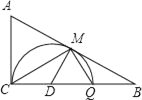
DM⊥AB，且AC=AM=5，

∴MB=AB﹣AM=13﹣5=8；

设CD=x，则DM=x，DB=12﹣x；

在Rt△DMB中，DB2=DM2+MB2，

即（12﹣x）2=x2+82，

解之得x=，

∴CQ=2x=；

即当CQ=且点P运动到切点M位置时，△CPQ为直角三角形．

②当＜CQ＜12时，半圆D与直线AB有两个交点，当点P运动到这两个交点的位置时，△CPQ为直角三角形

③当0＜CQ＜时，半圆D与直线AB相离，即点P在AB边上运动时，均在半圆D外，∠CPQ＜90°，此时△CPQ不可能为直角三角形．

∴当≤CQ＜12时，△CPQ可能为直角三角形．