题目内容
【题目】如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
(1)四边形EFGH是怎样的四边形?证明你的结论.
(2)当四边形ABCD的对角线AC、BD满足条件 时,四边形EFGH是矩形.
(3)当四边形ABCD的对角线AC、BD满足条件 时,四边形EFGH是菱形.

【答案】(1)平行四边形,证明见解析;(2)AC⊥BD;(3)AC=BD
【解析】
(1)根据三角形的中位线定理,可以证明所得四边形的两组对边分别和两条对角线平行,所得四边形的两组对边分别是两条对角线的一半,再根据平行四边形的判定就可证明该四边形是一个平行四边形;
(2)在(1)的基础上,所得四边形要成为矩形,则需有一个角是直角,故对角线应满足互相垂直;
(3)在(1)的基础上,所得四边形要成为菱形,则需有一组邻边相等,故对角线应满足相等.
解:(1)∵E、F、G、H分别是AB、BC、CD、DA边上的中点,
∴EF∥AC,EF=![]() AC,FG∥BD,FG=
AC,FG∥BD,FG=![]() BD,GH∥AC,GH=
BD,GH∥AC,GH=![]() AC,EH∥BD,EH=
AC,EH∥BD,EH=![]() BD.
BD.
∴EF∥HG,EF=GH,FG∥EH,FG=EH.
∴四边形EFGH是平行四边形;
(2)要使四边形EFGH是矩形,则需EF⊥FG,由(1)得,只需AC⊥BD;
故答案为:AC⊥BD;
(3)要使四边形EFGH是菱形,则需EF=FG,由(1)得,只需AC=BD;
故答案为:AC=BD.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案【题目】2018年10月17日是我国第五个“扶贫日”,某校学生会干部对学生倡导的“扶贫”自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图,(图中信息不完整),已知A.B两组捐款人数的比为1:5.
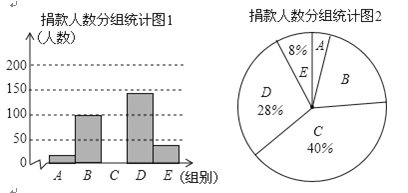
被调查的捐款人数分组统计表:
组别 | 捐款额x/元 | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | ______ |
D | 30≤x<40 | ______ |
E | 40≤x | ______ |
请结合以上信息解答下列问题:
(1)求a的值和参与调查的总人数;
(2)补全“被调查的捐款人数分组统计图1”并计算扇形B的圆心角度数;
(3)已知该校有学生2200人,请估计捐款数不少于30元的学生人数有多少人?






