题目内容
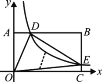
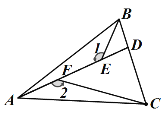
【题目】如图,△ABC为等腰三角形,AB=AC,AB>BC,∠1=∠2≠90°,∠1+∠BAC=180°,点A、F、E、D在一条直线上,点D在BC边上,CD=2BD.若△ABC的面积为40,求△ABE与△CDF的面积之和________
【答案】![]()
【解析】
先证明△ABE≌△CAF(AAS),再得到△ABE与△CDF的面积之和即为△ADC的面积,再求△ADC的面积即可.
∵∠1=∠2≠90°,∠1+∠BAC=180°,
∴∠2+∠BAC=180°,
又∵∠2+∠FAC+∠FCA=180°,
∴∠BAC=∠FAC+∠FCA,
又∵∠BAC=∠BAE+∠FAC,
∴∠BAE+∠FAC=∠FAC+∠FCA,
∴∠BAE=∠FCA,
在△ABE和△CAF中
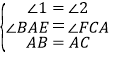 ,
,
∴△ABE≌△CAF(AAS),
∴△ABE与△CDF的面积之和为S△ADC。
∵点D在BC边上,CD=2BD.若△ABC的面积为40,
∴S△AD=![]() .
.
∴△ABE与△CDF的面积之和为![]()
故答案是:![]() .
.

练习册系列答案
相关题目