题目内容
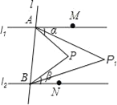
【题目】如图,直线l1∥l2,直线l与l1、l2分别交于A、B两点,点M、N分别在l1、l2上,点M、N、P均在l的同侧(点P不在l1、l2上),若∠PAM=α,∠PBN=β.
(1)当点P在l1与l2之间时.
①求∠APB的大小(用含α、β的代数式表示);
②若∠PAM的平分线与∠PBN的平分线交于点P1,∠P1AM的平分线与∠P1BN的平分线交于点P2,…,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn,则∠AP1B= ,∠APnB= .(用含α、β的代数式表示,其中n为正整数)
(2)当点P不在l1与l2之间时.
若∠PAM的平分线与∠PBN的平分线交于点P,∠P1AM的平分线与∠P1BN的平分线交于点P2,…,∠Pn﹣1AM的平分线与∠Pn﹣1BN的平分线交于点Pn,请直接写出∠APnB的大小.(用含α、β的代数式表示,其中n为正整数)
【答案】(1)①∠APB=α+β; ②∠AP1B=![]() (α+β);∠APnB=
(α+β);∠APnB=![]() ;(2)∠ApnB=
;(2)∠ApnB= ![]()
【解析】
(1)过点P作PQ∥l1交AB于Q,则∠APQ=∠MAP=α,由∠APQ=∠MAP=α①,∠QPB=∠PBN=β②,①+②即可解决问题.
(2)利用(1)的结论即可解决问题,分两种情形写出结论即可.
(1)①过点P作PQ∥l1交AB于Q,则∠APQ=∠MAP=α … ①
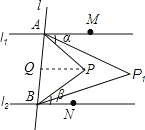
∵l1∥l2,
∴PQ∥l2,
∴∠QPB=∠PBN=β … ②,
①+②得∠APQ+∠BPQ=∠MAP+∠PBN,
∴∠APB=α+β.
由上可知∠P1=![]() (α+β),∠p2=
(α+β),∠p2=![]() (α+β),∠p3=
(α+β),∠p3=![]() (α+β)
(α+β)
∴∠APnB=![]() .
.
故∠AP1B=![]() (α+β);∠APnB=
(α+β);∠APnB=![]()
(2)当P在l1上方时,β>α,∠APnB=![]() .
.
当点P在l2下方时,α>β,∠ApnB=![]() .
.
故 ∠ApnB= ![]()

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案