题目内容
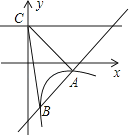
【题目】如图:在平面直角坐标系中,![]() 、
、![]() 两点的坐标分别为
两点的坐标分别为![]() 、
、![]() ,
,![]() 、
、![]() 分别是
分别是![]() 轴、
轴、![]() 轴上的点.如果以点
轴上的点.如果以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,则
为顶点的四边形是平行四边形,则![]() 的坐标为__________.
的坐标为__________.
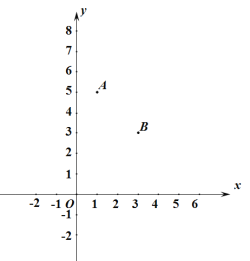
【答案】(2,0),(-2,0)(4,0)
【解析】
先把直线AB解析式和线段AB的长度计算出来,因此得到AB所在直线与x轴所成的度数,再根据平行四边形的定义寻找合适的点即可得到答案.
解:∵![]() 、
、![]() 两点的坐标分别为
两点的坐标分别为![]() 、
、![]() ,
,
∴![]() ,
,
设直线AB解析式为:![]() ,则:
,则:
![]()
解得![]() ,
,
∴![]() ,
,
∴直线与x轴的所形成的角是45°,
如果以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,且
为顶点的四边形是平行四边形,且![]() 、
、![]() 分别是
分别是![]() 轴、
轴、![]() 轴上的点,当AB为平行四边形的一边时,则MN∥AB,
轴上的点,当AB为平行四边形的一边时,则MN∥AB,
![]() ,
,
∴MN与x轴形成的角度是45°,
∵∠MON=90°,∴∠OMN=45°,
∴△MON是等腰直角三角形,
∴![]() ,
,
所以![]() 或
或![]() ;
;
当AB为平行四边形的对角线时,如图连接MN,MN与AB相交于点C,
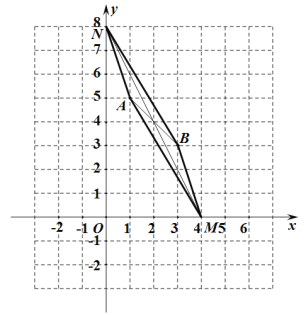
则C是AB、MN的中点,它的坐标为![]() ,
,
∴![]() ,
,
故答案为:(2,0),(-2,0)(4,0).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目