题目内容
【题目】如图,抛物线与x轴交于点和A(﹣1,0)和点B(4,0),与y轴交于点C(0,2).
(1)求抛物线解析式;
(2)点P是抛物线BC段上一点,PD⊥BC,PE∥y轴,分别交BC于点D、E.当DE= ![]() 时,求点P的坐标;
时,求点P的坐标;
(3)M是平面内一点,将符合(2)条件下的△PDE绕点M沿逆时针方向旋转90°后,点P,D,E的对应点分别是P′、D′、E′.设P′E′的中点为N,当抛物线同时经过D′与N时,求出D′的横坐标.
【答案】
(1)解:设y=a(x+1)(x﹣4),把C(0,2)代入解得a= ![]()
∴y=﹣ ![]() (x+1)(x﹣4)=﹣
(x+1)(x﹣4)=﹣ ![]() x2+
x2+ ![]() x+2.
x+2.
(2)解:如图1所示:延长PE交x轴与点F.
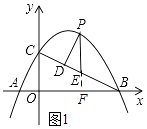
∵OC=2,OB=4,
∴BC= ![]() =2
=2 ![]() .
.
∵PD⊥BC,CO⊥OB,
∴∠COB=∠PDE=90°.
∵∠PDE=∠EFB,∠PED=∠FEB,
∴∠DPE=∠CBO.
∴△PDE∽△BOC.
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得PE=2.
,解得PE=2.
设BC的解析式为y=kx+2,将点B的坐标代入得:4k+2=0,解得:k=﹣ ![]() .
.
∴直线BC的解析式为y=﹣ ![]() x+2.
x+2.
设点P的坐标为(x,﹣ ![]() x2+
x2+ ![]() x+2),则E(x,﹣
x+2),则E(x,﹣ ![]() x+2).
x+2).
∴﹣ ![]() x2+
x2+ ![]() x+2﹣(﹣
x+2﹣(﹣ ![]() x+2)=2,解得x1=x2=2.
x+2)=2,解得x1=x2=2.
∴点P的坐标为(2,3).
(3)解:旋转后的图形如图2所示:过点D′作D′H⊥P′E′,垂足为H.

∵∠P'D'E'=90°,N是斜边P'E'的中点,
∴D′B= ![]() P′E′=1.
P′E′=1.
∵ ![]() P′D′E′D′=
P′D′E′D′= ![]() P′E′HD′,
P′E′HD′,
∴D′H= ![]() =
= ![]() =
= ![]() .
.
∴HP′= ![]() .
.
∴HN=P′H﹣P′N= ![]() .
.
设D′(x,﹣ ![]() x2+
x2+ ![]() x+2),则N(x﹣
x+2),则N(x﹣ ![]() ,﹣
,﹣ ![]() x2+
x2+ ![]() x+2+
x+2+ ![]() ),
),
把N点坐标代入抛物线得﹣ ![]() x2+
x2+ ![]() x+2+
x+2+ ![]() =﹣
=﹣ ![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() (x﹣
(x﹣ ![]() )+2,解得:x=
)+2,解得:x= ![]() .
.
∴点D′的横坐标为 ![]() .
.
【解析】(1)由题意可设此二次函数的解析式为y=a(x+1)(x﹣4),把C点的坐标代入可求得;
(2)易求出BC的长,再证△PDE∽△BOC,利用对应边成比例可求得PE的长,利用待定系数法求出直线BC的解析式,从而设出P、E的坐标,进而求出答案;
(3)根据题意画出图形,再过点D′作D′H⊥P′E′,利用直角三角形的性质可得BD′,由三角形的面积公式可求得HD′,进而求得HN的值,设D′![]() ,可得N点的坐标,把N点的坐标代入抛物线可求得x的值,即可得答案.
,可得N点的坐标,把N点的坐标代入抛物线可求得x的值,即可得答案.
【考点精析】关于本题考查的相似三角形的判定与性质,需要了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.

 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案【题目】某商场甲、乙、丙三名业务员5个月的销售额(单位:万元)如下表:
月份 | 第1月 | 第2月 | 第3月 | 第4月 | 第5月 |
甲 | 7.2 | 9.6 | 9.6 | 7.8 | 9.3 |
乙 | 5.8 | 9.7 | 9.8 | 5.8 | 9.9 |
丙 | 4 | 6.2 | 8.5 | 9.9 | 9.9 |
(1)根据上表中的数据,将下表补充完整:
统计值 | 平均数(万元) | 中位数(万元) | 众数(万元) |
甲 | 9.3 | 9.6 | |
乙 | 8.2 | 5.8 | |
丙 | 7.7 | 8.5 |
(2)甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法?请说明理由.