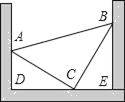
题目内容
【题目】如图,在菱形ABCD中,∠A=110°,点E是菱形ABCD内一点,连结CE绕点C顺时针旋转110°,得到线段CF,连结BE,DF,若∠E=86°,求∠F的度数.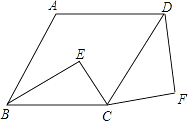
【答案】解:∵菱形ABCD,
∴BC=CD,∠BCD=∠A=110°,
由旋转的性质知,CE=CF,∠ECF=∠BCD=110°,
∴∠BCE=∠DCF=110°﹣∠DCE,
在△BCE和△DCF中, 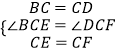 ,
,
∴△BCE≌△DCF,
∴∠F=∠E=86°.
【解析】由菱形的性质得出邻边相等,对角相等,旋转的性质可知CE=CF,证得△BCE≌△DCF,∠F可转化为∠E的度数.
【考点精析】解答此题的关键在于理解菱形的性质的相关知识,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半,以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目