题目内容
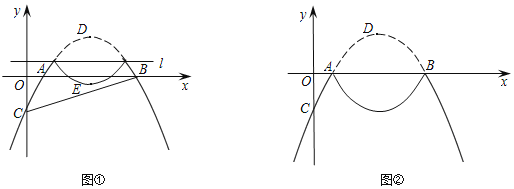
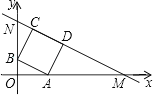
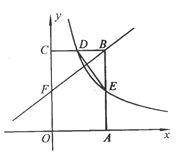
【题目】如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,4),双曲线![]() 的图像经过BC的中点D,且与AB交于点E,连接DE.
的图像经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△FBC∽△DEB,求直线FB的解析式.
【答案】(1)![]() ,(2,2);(2)y=2x
,(2,2);(2)y=2x
【解析】
(1)首先根据点B的坐标和点D为BC的中点表示出点D的坐标,代入反比例函数的解析式求得k值,然后将点E的横坐标代入求得E点的纵坐标即可;
(2)根据△FBC∽△DEB,利用相似三角形对应边的比相等确定点F的坐标后即可求得直线FB的解析式.
(1)∵BC∥x轴,点B的坐标为(2,4),
∴BC=2,
∵点D为BC的中点,
∴CD=1,
∴点D的坐标为(1,4),
代入双曲线![]() (x>0)得:k=1×4=4;
(x>0)得:k=1×4=4;
∵BA∥y轴,
∴点E的横坐标与点B的横坐标相等,为2,
∵点E在双曲线上,
∴y=2
∴点E的坐标为(2,2);
(2)∵点E的坐标为(2,2),B的坐标为(2,4),点D的坐标为(1,4),
∴BD=1,BE=2,BC=2
∵△FBC∽△DEB,
∴![]()
即:![]()
∴FC=1
∴点F的坐标为(0,2)
设直线FB的解析式![]() (k≠0)
(k≠0)
则![]()
解得:k=2,b=0
∴直线FB的解析式y=2x

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案【题目】为了解某区八年级学生的睡眠情况,随机抽取了该区八年级学生部分学生进行调查.已知D组的学生有15人,利用抽样所得的数据绘制所示的统计图表.
一、学生睡眠情况分组表(单位:小时)
组别 | 睡眠时间 |
|
|
|
|
|
|
|
|
|
|
二、学生睡眠情况统计图

根据图表提供的信息,回答下列问题:
(1)试求“八年级学生睡眠情况统计图”中的a的值及a对应的扇形的圆心角度数;
(2)如果睡眠时间x(时)满足:![]() ,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
(3)如果将各组别学生睡眠情况分组的最小值(如C组别中,取![]() ),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
【题目】某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:
成绩 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 1 | 11 | 7 | 1 |
乙 |
(说明:成绩80分及以上为生产技能优秀,70--79分为生产技能良好,60--69分为生产技能合格,60分以下为生产技能不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | 75 |
乙 | 78 | 80.5 | 81 |