Question

【题目】在由6个大小相同的小正方形组成的方格中：

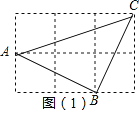
（1）如图（1），△ABC 的三个顶点A、B、C都在格点上，试判断△ABC的形状，并加以证明；

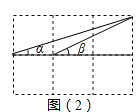
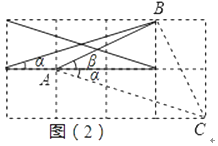
（2）如图（2），连结三格和两格的对角线，利用（1）的图形特征，求出∠α+∠β的度数．

Answer 1

【答案】（1）△ABC是等腰直角三角形，理由见详解；（2）∠α+∠β=45°，理由见详解.

【解析】

（1）如图（1），根据勾股定理，判断出AB2+BC2=AC2，即可推得△ABC是直角三角形，又AB=BC，即可得到结论．

（2）如图（2），根据勾股定理，判断出AB2+BC2=AC2，即可推得△ABC是等腰直角三角形，据此求出∠α+∠β的度数是多少即可．

解：（1）如图（1），

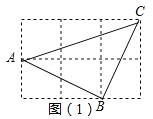
由勾股定理得，AB2=12+22=5，

BC2=12+22=5，

AC2=12+32=10，

∴AB2+BC2=AC2，AB=BC，

∴△ABC是等腰直角三角形；

（2）∠α+∠β=45°．

证明：如图（2），

，

由勾股定理得，AB2=12+22=5，

BC2=12+22=5，

AC2=12+32=10，

∴AB2+BC2=AC2，

∴△ABC是直角三角形，

∵AB=BC，

∴△ABC是等腰直角三角形，

∴∠α+∠β=45°．