题目内容
 如图,已知反比例函数
如图,已知反比例函数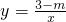 (m为常数)的图象经过点A(1,6).
(m为常数)的图象经过点A(1,6).
(1)求m的值;
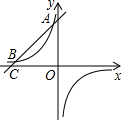
(2)过点A的直线交x轴于点B,交y轴于点C,且OC=OB,求直线BC的解析式.
解:(1)根据题意,将A的坐标代入反比例解析式得:3-m=1×6,
解得:m=-3;
(2)由OB=OC,故设直线BC的解析式为y=x+b,
∵点A(1,6)在直线BC上,
∴将x=1,y=6代入y=x+b得:1+b=6,
解得:b=5,
则直线BC的解析式为y=x+5.
分析:(1)由A为反比例函数图象上的点,将A的坐标代入反比例解析式中,即可求出m的值;
(2)由OB=OC,得到直线BC在坐标轴上的截距相等,故设直线BC解析式为y=x+b,再由A在直线BC上,将A的坐标代入y=x+b,求出b的值,即可确定出直线BC的解析式.
点评:此题考查了反比例函数与一次函数的交点问题,利用了待定系数法,待定系数法是数学中重要的思想方法,学生做题时注意灵活运用.
解得:m=-3;
(2)由OB=OC,故设直线BC的解析式为y=x+b,
∵点A(1,6)在直线BC上,
∴将x=1,y=6代入y=x+b得:1+b=6,
解得:b=5,
则直线BC的解析式为y=x+5.
分析:(1)由A为反比例函数图象上的点,将A的坐标代入反比例解析式中,即可求出m的值;
(2)由OB=OC,得到直线BC在坐标轴上的截距相等,故设直线BC解析式为y=x+b,再由A在直线BC上,将A的坐标代入y=x+b,求出b的值,即可确定出直线BC的解析式.
点评:此题考查了反比例函数与一次函数的交点问题,利用了待定系数法,待定系数法是数学中重要的思想方法,学生做题时注意灵活运用.

练习册系列答案
相关题目
 如图,已知反比例函数
如图,已知反比例函数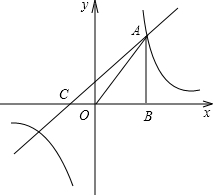 如图,已知反比例函数
如图,已知反比例函数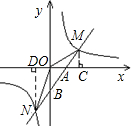 如图,已知反比例函数y=
如图,已知反比例函数y=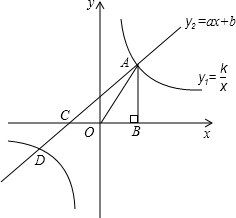 如图,已知反比例函数
如图,已知反比例函数 如图,已知反比例函数y=
如图,已知反比例函数y=