Question

【题目】如图，平行四边形ABCD的对角线AC和BD相交于点O ， E ， F分别为OB ， OD的中点，过点O任作一直线分别交AB ， CD于点G ， H.
试说明：GF∥EH.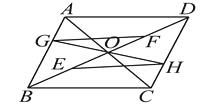

Answer 1

【答案】证明：连结EG ， FH ， 由□ABCD得
OA＝OC ， OB＝OD ，
又OE＝ OB ， OF＝ OD ，
∴OE＝OF ，
再证△AOG≌△COH得OG＝OH ，
∴四边形EHFG是平行四边形，
∴GF∥EH.
【解析】平行四边形的判定，方法共有五种，本题的条件为：平行四边形ABCD中，对角线AC、BD相交于点O ， 点E、F分别是OB、OD的中点，根据条件，本题应选择利用“对角线互相平分的四边形是平行四边形”来解决．
【考点精析】根据题目的已知条件，利用平行四边形的判定的相关知识可以得到问题的答案，需要掌握两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形．