题目内容
【题目】如图，已知□ABCD的对角线AC ， BD相交于点O ， 直线EF经过点O ， 且分别交AB ， CD于点E ， F.求证：四边形BFDE是平行四边形．．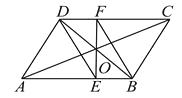
【答案】证明：∵□ABCD的对角线AC ， BD相交于点O ，
∴OA＝OC ， OB＝OD ， ∠DCO=∠BAO
又∵∠AOE=∠COD，
∴△AOE≌△COF ，
得OE＝OF ，
∴四边形BFDE是平行四边形．
【解析】由平行四边形的性质得到OA＝OC ， OB＝OD ， ∠DCO=∠BAO ， 再由ASA证得△AOE≌△COF ， 可推出OE＝OF ， 从而得到对角线互相平分的四边形是平行四边形．
【考点精析】根据题目的已知条件，利用平行四边形的判定的相关知识可以得到问题的答案，需要掌握两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形．
练习册系列答案
快捷英语周周练系列答案
相关题目
