��Ŀ����
����Ŀ��ij������˾����A��B���ֻ�������������ij�ֻ�������ֻ����˳�����������������5Сʱ��A�ֻ�������ij��0ʱ��ʼ���ˣ�����1Сʱ��B�ֻ�����Ҳ��ʼ���ˣ���ͼ���߶�OG��ʾA�ֻ����˵İ�����yA��ǧ�ˣ���ʱ��x��ʱ���ĺ���ͼ����ͼ���ṩ����Ϣ������������⣺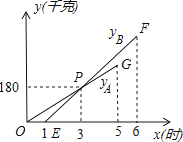
��1����yB����x�ĺ�������ʽ��
��2�����A��B���ֻ�������������5��Сʱ����ôB�ֻ����˱�A�ֻ����˶�����˶���ǧ�ˣ�
���𰸡�
��1��
�⣺��yB����x�ĺ�������ʽΪyB=kx+b��k��0����
���㣨1��0������3��180������ã� ![]() ��
��
��ã�k=90��b=��90��
����yB����x�ĺ�������ʽΪyB=90x��90��1��x��6��
��2��
�⣺��yA����x�Ľ���ʽΪyA=k1x��
��������ã�3k1=180��
��ã�k1=60��
����yA=60x��
��x=5ʱ��yA=60��5=300��ǧ�ˣ���
x=6ʱ��yB=90��6��90=450��ǧ�ˣ���
450��300=150��ǧ�ˣ���
������A��B���ֻ����˸���������5Сʱ��B�ֻ����˱�A�ֻ����˶������150ǧ��
����������1����yB����x�ĺ�������ʽΪyB=kx+b��k��0�������㣨1��0������3��180������һ�κ��������Ľ���ʽ�õ�����k��b�ķ����飬�Ӷ�����ú����Ľ���ʽ��
��2����yA����x�Ľ���ʽΪyA=k1x������3��180����������yA����x�Ľ���ʽ��Ȼ��x=6��x=5����һ�κ����������������Ľ���ʽ���yA �� yB��ֵ��������yA��yB�IJ�ɣ� ������Ҫ�������һ�κ�����Ӧ�ã����ݴ���ϵ�������һ�κ����Ľ���ʽ�ǽ���Ĺؼ���

 ��ǰ����ϵ�д�
��ǰ����ϵ�д�