��Ŀ����
����Ŀ�����ж��ص�������Դ����Ȼ���ֵ�������������Ԫ�д����ƹ��߲���ֲ����������ڼ䣬ij�߲���ֲ����ͨ������ƽ̨���߲�����ȫ�����أ�����������������û���Ϊ����߲˲������ƻ��Լס��������ͺ��߲˴�����и��죬����Ԥ�㣬����2�������ͺŴ����1�������ͺŴ�������ʽ�6��Ԫ������1�������ͺŴ����2�������ͺŴ��ﹲ���ʽ�48��Ԫ��
��1�������1�������ͺź�1�������ͺŴ��������ʽ�ֱ��Ƕ�����Ԫ��
��2����֪����1�������ͺŴ�����Ҫ5�죬����1�������ͺŴ�����Ҫ3�죬�û��ؼƻ���126��Ԫ�ʽ����һ�������������ͺ��߲˴����Ҫ�����ʱ���ܹ�������50�죬���ʣ��м��ָ��췽�������ַ�������ʱ����̣�
���𰸡���1������1�������ͺŴ�����12��Ԫ������1�������ͺŴ�����18��Ԫ����2����3�ָ��췽�������и���3�������ͺŴ������5�������ͺŴ����������ʱ�����
��������
��1��������������ȹ�ϵ������2�������ͺŴ���ķ��ã�����1�������ͺŴ���ķ���=6��Ԫ������1�������ͺŴ���ķ���+����2�������ͺŴ���ķ���=48��Ԫ���ݴ���δ֪���з������ɣ�
��2�����������ͺŴ���a�������������ͺŴ���b�����ɸ����ʽ�126��Ԫ�ɵù���a��b�ķ��̣��������ú�a�Ĵ���ʽ��ʾb���ɸ���ʱ���ܹ�������50��ɵù���a�IJ���ʽ���Ӷ������a��ȡֵ��Χ��Ȼ�����һ�κ��������ʼ����������ʱ�����Сֵ��
�⣺��1�������1�������ͺŴ�����x��Ԫ������1�������ͺŴ�����y��Ԫ��
�����⣬��![]() ����ã�
����ã�![]() ��
��
�𣺸���1�������ͺŴ�����12��Ԫ������1�������ͺŴ�����18��Ԫ��
��2�����������ͺŴ���a�������������ͺŴ���b����
�����⣬��12a+18b=126����b=7��![]() a��
a��
�����⣬��5a+3![]() ��50����ã�a��
��50����ã�a��![]() ��
��
��a��b��������
��a��ֵΪ3��6��9�����Թ���3�ָ��췽����
�����ʱ��Ϊw�죬��w=5a+3![]() =3a+21��
=3a+21��
��3��0���൱a=3ʱ��wȡ����Сֵ����ʱb=5��
����3�ָ��췽�������и���3�������ͺŴ������5�������ͺŴ����������ʱ����̣�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��Ϊ���˽�ͬѧ��ÿ���㻨Ǯ�����УС������������˱�У����ͬѧ�����ݵ������������������в�������ͳ��ͼ����
��� | A | B | C | D | E |
���飨Ԫ�� | 0��x<30 | 30��x<60 | 60��x<90 | 90��x<120 | 120��x<150 |
Ƶ�� | 4 | a | 20 | 8 | 2 |
���������ͼ�꣬����������⣺
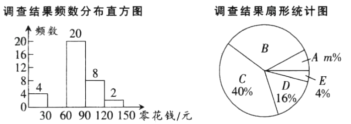
��1����գ���ε�������������� ��a= ��m= ��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3��������ͳ��ͼ������B��Բ�ĽǶ�����
��4����У����1000�ˣ������ÿ���㻨Ǯ������x��30��x<90��Χ��������
����Ŀ���±���¼�˼ס��ҡ�����������ͬѧ���������ѧ���Գɼ���ƽ�����뷽����ݱ������ݣ�Ҫ����ѡ��һ���ɼ����ҷ����ȶ���ͬѧ�μ���ѧ������Ӧ��ѡ��__________������������ �������� �������� ����������
�� | �� | �� | �� | |
ƽ�������֣� | 92 | 95 | 95 | 92 |
���� | 3.6 | 3.6 | 7.4 | 8.1 |