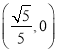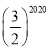题目内容
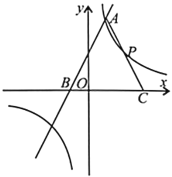
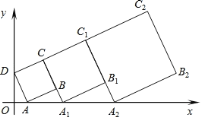
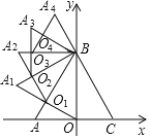
【题目】如图，边长为4的等边△ABC，AC边在x轴上，点B在y轴的正半轴上，以OB为边作等边△OBA1，边OA1与AB交于点O1，以O1B为边作等边△O1BA2，边O1A2与A1B交于点O2，以O2B为边作等边△O2BA3，边O2A3与A2B交于点O3，…，依此规律继续作等边△On﹣1BAn，则
的横坐标_____．
【答案】
【解析】
由题意：△OO1A∽△O1O2A1∽△O2O3A2，…，∽△On-1OnAn-1，相似比：
，探究规律，利用规律即可解决问题．
∵边长为4的等边△ABC，AC边在x轴上，点B在y轴的正半轴上，OB⊥AC，
∴∠BAC=∠ABC=60°，
，
∴
，
，
∵以OB为边作等边△OBA1，边OA1与AB交于点O1，以O1B为边作等边△O1BA2，边O1A2与A1B交于点O2，
∴∠BA1O=∠A1OB=∠A2O1B=60°，
，
∴∠AOO1=∠A1O1O2=90°-60°=30°，
在△OO1A与△O1O2A1中，
，
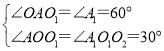∴△OO1A∽△O1O2A1，
同理，可得△OO1A∽△O1O2A1∽△O2O3A2∽…∽△On-1OnAn-1，相似比：
，
∵∠OBA=∠O1BA1=∠O2BA2=∠O3BA3=…=∠O1BA1=On-1BAn-1=30°，360°÷30°=12，
∴这些点所在的位置以360°÷30°=12个为一个周期依次循环，
∵2020÷12=168……4，
∴A2020的横坐标为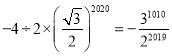
．
故答案为：．
练习册系列答案
步步高达标卷系列答案
相关题目
