题目内容
如下图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为点D,CE平分∠ACB,交AD于点G,交AB于点E,EF⊥BC,垂足为F,求证:四边形AEFG是菱形.

答案:
解析:
解析:
|
证明:∵∠1=∠B+∠4 ∠2=∠3+∠5 又∵∠BAC=90° AD⊥BC ∴∠5=∠B ∴CE平分∠ACB ∴∠3=∠4 ∴∠1=∠2 ∴AE=AG ∵EF⊥BC ∠BAC=90° ∴AE=EF ∵AD⊥BC,EF⊥BC ∴EF//AD ∵EF=AG ∴四边形AGFE为平行四边形 ∵AE=EF ∴四边形AGFE为菱形 |

练习册系列答案
相关题目
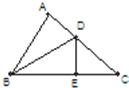 2、如下图,在△ABC中,∠A=90°,BD是∠ABC的平分线,DE是BC的垂直平分线,若AD=2cm,则CD=
2、如下图,在△ABC中,∠A=90°,BD是∠ABC的平分线,DE是BC的垂直平分线,若AD=2cm,则CD=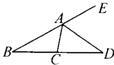 25、如下图,在△ABC中,AD平分外角∠CAE,∠B=30°,∠CAD=65°,则∠ACD等于( )
25、如下图,在△ABC中,AD平分外角∠CAE,∠B=30°,∠CAD=65°,则∠ACD等于( )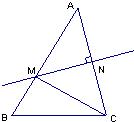 16、如下图,在△ABC中,AB=8,BC=6,AC的垂直平分线MN交AB、AC于点M、N.则△BCM的周长为
16、如下图,在△ABC中,AB=8,BC=6,AC的垂直平分线MN交AB、AC于点M、N.则△BCM的周长为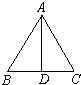 18、已知如下图,在△ABC中,AB=AC,AD⊥BC,垂足为D,则图中相等的线段还有
18、已知如下图,在△ABC中,AB=AC,AD⊥BC,垂足为D,则图中相等的线段还有 如下图,在△ABC中,∠C=30°,∠ABC=90°,AC∥BD,则∠ABD=
如下图,在△ABC中,∠C=30°,∠ABC=90°,AC∥BD,则∠ABD=