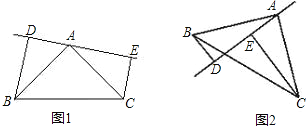
题目内容
【题目】如图1,![]() ,
,![]() ,
,![]() .
.

(1)求![]() 的度数的大小;
的度数的大小;
(2)如图2,若![]() 连接
连接![]() ,请判断直线
,请判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)如图2,根据(2)问的条件,连接![]() 与直线
与直线![]() 交于点
交于点![]() ,若
,若![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() 的度数为45°;(2)
的度数为45°;(2)![]() ,见解析;(3)
,见解析;(3)![]() .
.
【解析】
(1)连接AB,过D作DT∥AE,则DT∥BF,由直角三角形的性质得出∠CAB+∠CBA=90°,由平行线的性质得出∠BAE+∠ABF=180°,得出∠CAE+∠CBF=90°,由角平分线得出∠CAD=∠EAD,∠CBD=∠FBD,证出∠EAD+∠FBD=45°,由平行线的性质得出∠TDA=∠EAD,∠TDB=∠FBD,得出∠TDA+∠TDB=45°即可;
(2)证明△ACD≌△BCD得出∠CDA=∠CDB,证出∠DAC=67.5°-45°=22.5°,进一步得出∠CDA=∠EAD,即可得出结论;
(3)证明△AGC是等腰直角三角形,得出CG=AG=3,由三角形面积公式即可得出结果.
(1)连接AB,过D作DT∥AE,则DT∥BF,如图1所示:
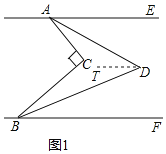
∵∠ACB=90°,
∴∠CAB+∠CBA=90°,
∵AE∥BF,
∴∠BAE+∠ABF=180°,
∴∠CAE+∠CBF=90°,
∵∠AD、BD分别是∠EAC、∠FBC的角平分线,
∴∠CAD=∠EAD,∠CBD=∠FBD,
∵∠CAD+∠EAD+∠CBD+∠FBD=90°,
∴∠EAD+∠FBD=45°,
∵DT∥AE,
∴∠TDA=∠EAD,
∵DT∥BF,
∴∠TDB=∠FBD,
∴∠TDA+∠TDB=45°,
∴∠ADB=45°;
(2)CD∥AE;理由如下:
∵AC=BC,
∴∠CAB=∠CBA,
∵AD=BD,
∴∠DAB=∠DBA,
∴∠DAC=∠DBC,
在△ACD和△BCD中,
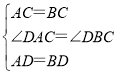 ,
,
∴△ACD≌△BCD(SAS),
∴∠CDA=∠CDB,
∵∠ADB=45°,
∴∠CDA=22.5°,∠BAD=67.5°,
∵∠ACB=90°,AC=BC,
∴∠CAB=45°,
∴∠DAC=67.5°-45°=22.5°,
∵AD平分∠EAC,
∴∠EAD=∠DAC=22.5°,
∴∠CDA=∠EAD,
∴CD∥AE;
(3)∵∠CDA=∠CDB,AD=BD,
∴DG⊥AB,AG=BG=![]() AB=3,
AB=3,
∵∠CAB=45°,
∴△AGC是等腰直角三角形,
∴CG=AG=3,
∴S△ABC=![]() ABCG=
ABCG=![]() ×6×3=9.
×6×3=9.