题目内容
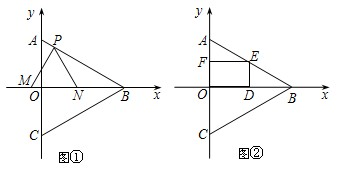
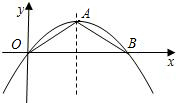
如图,抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.
(1)求抛物线的解析式;
(2)在抛物线上求点M,使△MOB的面积是△AOB面积的3倍.
(1)求抛物线的解析式;
(2)在抛物线上求点M,使△MOB的面积是△AOB面积的3倍.

(1)由题意,可设抛物线的解析式为y=a(x-2)2+1,(2分)
∵抛物线过原点,
∴a(0-2)2+1=0,a=-
;(2分)
∴抛物线的解析式为y=-
(x-2)2+1=-
x2+x.(1分)
(2)△AOB和所求△MOB同底不等高,且S△MOB=3S△AOB,
∴△MOB的高是△AOB高的3倍,
即M点的纵坐标是-3,(3分)
∴-3=-
x2+x,
即x2-4x-12=0,(1分)
解之,得x1=6,x2=-2,(2分)
∴满足条件的点有两个:M1(6,-3),M2(-2,-3).(1分)
∵抛物线过原点,
∴a(0-2)2+1=0,a=-
| 1 |
| 4 |
∴抛物线的解析式为y=-
| 1 |
| 4 |
| 1 |
| 4 |
(2)△AOB和所求△MOB同底不等高,且S△MOB=3S△AOB,
∴△MOB的高是△AOB高的3倍,
即M点的纵坐标是-3,(3分)
∴-3=-
| 1 |
| 4 |
即x2-4x-12=0,(1分)
解之,得x1=6,x2=-2,(2分)
∴满足条件的点有两个:M1(6,-3),M2(-2,-3).(1分)

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 若不存在,请说明理由.
若不存在,请说明理由.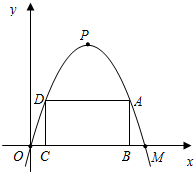
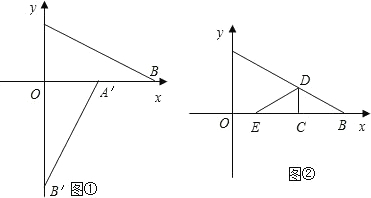
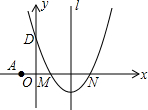 两点,且与y轴交于D(0,3),直线l是抛物线的对称轴.
两点,且与y轴交于D(0,3),直线l是抛物线的对称轴.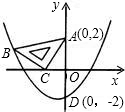 和点C,与抛物线y=ax2+ax+b交于点B,其中点A(0,2),点B(-3,1),抛物线与y轴交点D(0,-2).
和点C,与抛物线y=ax2+ax+b交于点B,其中点A(0,2),点B(-3,1),抛物线与y轴交点D(0,-2).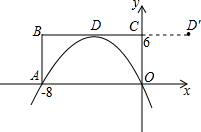 过A、D两点,如图所示.
过A、D两点,如图所示.