题目内容
【题目】如图,四边形ABCD内接于⊙O,AC⊥BD于E.
(1)用尺规作图作DF⊥AB于F,交AC于G,并标出F、G(保留作图痕迹,不写作法);
(2)在(1)中,若∠BAD=45°,求证:EG=EC.
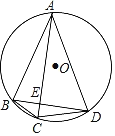
【答案】(1)答案见解析;(2)证明见解析.
【解析】
(1)根据题意作出图形即可;
(2)根据垂直的定义得到∠GED=∠DEC=90°,根据相似三角形的性质得到∠BAE=∠BDF,根据全等三角形的性质即可得到结论.
解:(1)如图所示;
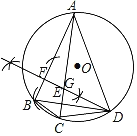
(2)证明:∵AC⊥BD,DF⊥AB,
∴∠BFD=∠AEB=90°,
即∠GED=∠DEC=90°,
∵∠B=∠B,
∴△ABE∽△DBF,
∴∠BAE=∠BDF,
∵∠BAE=∠BDC,
∴∠BDC=∠BDF,
∵DE=DE,
∴△DGE≌△DCE(ASA),
∴GE=CE.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案
相关题目