题目内容
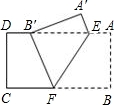
如图，矩形ABCD中，点E在AB上，现沿EC翻折，使点B刚好落在AD上的F点，若AB=3，BC=5．则折痕EC=（ ）
A．
| B．2
| C．
| D．
|
设BE=EF=x，则AE=3-x，
∵CF=CB=5，CD=3，
在Rt△CDF中，根据勾股定理可知DF=4，
∴AF=1，
在Rt△AEF中，利用勾股定理得：AF2+AE2=EF2，即12+（3-x）2=x2，
解得：x=
，即BE=
，
在Rt△BCE中，利用勾股定理可知：BE2+BC2=EC2，
代入解得：EC=
．
故选C．
∵CF=CB=5，CD=3，
在Rt△CDF中，根据勾股定理可知DF=4，
∴AF=1，
在Rt△AEF中，利用勾股定理得：AF2+AE2=EF2，即12+（3-x）2=x2，
解得：x=
| 5 |
| 3 |
| 5 |
| 3 |
在Rt△BCE中，利用勾股定理可知：BE2+BC2=EC2，
代入解得：EC=
5
| ||
| 3 |
故选C．
练习册系列答案
长江作业本同步练习册系列答案
小天才课时作业系列答案
一课四练系列答案
相关题目
