题目内容
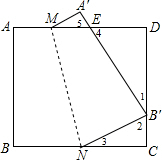
如图,四边形ABCD是边长为9的正方形纸片,沿MN折叠,使点B落在CD边上的B′处,点A对应点A′,且B′C=3,求CN和AM的长.


如图,
∵边长为9的正方形纸片,沿MN折叠,使点B落在CD边上的B′处,点A对应点A′,
∴A′B′=AB=9,NB′=NB,∠NB′A′=∠B=90°,
设CN=x,则NB=9-x,NB′=9-x,
在Rt△NCB′,B′C=3,
∵NC2+B′C2=NB′2,
∴x2+32=(9-x)2,解得x=4,
∴CN=4,NB′=9-4=5,
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
∴Rt△B′DE∽Rt△NCB′,
∴
=
=
,
而DB′=DC-CB′=6,
∴
=
=
,
∴DE=
,B′E=
,
∴A′E=A′B′-B′E=9-
=
,
∵∠5=∠4,
∴Rt△MA′E∽Rt△B′DE,
∴
=
,即
=
,
∴ME=
,
∴AM=AD-ME-DE=9-
-
=2,
故CN的长为4,AM的长为2.
∵边长为9的正方形纸片,沿MN折叠,使点B落在CD边上的B′处,点A对应点A′,
∴A′B′=AB=9,NB′=NB,∠NB′A′=∠B=90°,
设CN=x,则NB=9-x,NB′=9-x,
在Rt△NCB′,B′C=3,
∵NC2+B′C2=NB′2,
∴x2+32=(9-x)2,解得x=4,
∴CN=4,NB′=9-4=5,
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
∴Rt△B′DE∽Rt△NCB′,
∴
| DB′ |
| NC |
| DE |
| B′C |
| B′E |
| NB′ |
而DB′=DC-CB′=6,
∴
| DE |
| 3 |
| B′E |
| 5 |
| 6 |
| 4 |
∴DE=
| 9 |
| 2 |
| 15 |
| 2 |
∴A′E=A′B′-B′E=9-
| 15 |
| 2 |
| 3 |
| 2 |
∵∠5=∠4,
∴Rt△MA′E∽Rt△B′DE,
∴
| ME |
| B′E |
| A′E |
| DE |
| ME | ||
|
| ||
|
∴ME=
| 5 |
| 2 |
∴AM=AD-ME-DE=9-
| 5 |
| 2 |
| 9 |
| 2 |
故CN的长为4,AM的长为2.


练习册系列答案
相关题目
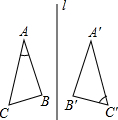




 把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E.
把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E.