题目内容
如图，把矩形纸片ABCD沿EF折叠，使点B落在边AD上的点B′处，点A落在点A处，则AE、AB、BF之间的关系是______．
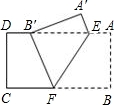
由折叠的性质知：A′B′=AB，AE=A′E，BF=B′F，∠A′=∠A=90°，∠B′FE=∠BFE；
又∵AD∥BC，∴∠BFE=∠B′EF，
∴∠B′EF=∠BFE=∠B′FE，即B′E=B′F=BF；
在Rt△A′B′E中，由勾股定理得：A′B′2+A′E2=B′E2，
即：AE2+AB2=BF2．
又∵AD∥BC，∴∠BFE=∠B′EF，
∴∠B′EF=∠BFE=∠B′FE，即B′E=B′F=BF；
在Rt△A′B′E中，由勾股定理得：A′B′2+A′E2=B′E2，
即：AE2+AB2=BF2．
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
180°，得到△AB′C．
