题目内容
为了探索代数式
+
的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则AC=
,CE=
,则问题即转化成求AC+CE的最小值.
(1)我们知道当A、C、E在同一直线上时,AC+CE的值最小,于是可求得
+
的最小值等于______,此时x=______;
(2)请你根据上述的方法和结论,试构图求出代数式
+
的最小值.

| x2+1 |
| (8-x)2+25 |
| x2+1 |
| (8-x)2+25 |
(1)我们知道当A、C、E在同一直线上时,AC+CE的值最小,于是可求得
| x2+1 |
| (8-x)2+25 |
(2)请你根据上述的方法和结论,试构图求出代数式
| x2+4 |
| (12-x)2+9 |

(1)过点E作EF∥BD,交AB的延长线于F点,
根据题意,四边形BDEF为矩形.
AF=AB+BF=5+1=6,EF=BD=8.
∴AE=
=10.
即AC+CE的最小值是10.
+
=10,
∵EF∥BD,
∴
=
,
∴
=
,
解得:x=
.
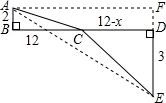 (2)过点A作AF∥BD,交DE的延长线于F点,
(2)过点A作AF∥BD,交DE的延长线于F点,
根据题意,四边形ABDF为矩形.
EF=AB+DE=2+3=5,AF=DB=12.
∴AE=
=13.
即AC+CE的最小值是13.

根据题意,四边形BDEF为矩形.
AF=AB+BF=5+1=6,EF=BD=8.
∴AE=
| 62+82 |
即AC+CE的最小值是10.
| x2+1 |
| (8-x)2+25 |
∵EF∥BD,
∴
| AB |
| AF |
| BC |
| EF |
∴
| 1 |
| 6 |
| x |
| 8 |
解得:x=
| 4 |
| 3 |
 (2)过点A作AF∥BD,交DE的延长线于F点,
(2)过点A作AF∥BD,交DE的延长线于F点,根据题意,四边形ABDF为矩形.
EF=AB+DE=2+3=5,AF=DB=12.
∴AE=
| 52+122 |
即AC+CE的最小值是13.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 180°,得到△AB′C.
180°,得到△AB′C.



 把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E.
把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E.
