Question

【题目】如图，在△ABC中，∠ACB＝90°，CD⊥AB于点D，点E是直线AC上一动点，连接DE，过点D作FD⊥ED，交直线BC于点F.

(1)如图1，当点E在线段AC上时，求证：△DEC∽△DFB.

(2)当点E在线段AC的延长线上时，(1)中的结论是否仍然成立？若成立，请结合图2给出证明；若不成立，请说明理由；

(3)若AC＝，BC＝2，DF＝4，请直接写出CE的长.

Answer 1

【答案】(1)证明见解析；(2)成立，理由见解析；(3)CE＝2或CE＝.

【解析】

(1)首先证明∠ACD＝∠B，∠EDC＝∠BDF，得到△DEC∽△DFB.

(2)方法和(1)一样，首先证明∠ACD＝∠B，∠EDC＝∠BDF，得到△DEC∽△DFB.

(3)由(2)的结论得出△ADE∽△CDF，判断出CF＝2AE，求出EF，再利用勾股定理，分三种情形分别求解即可.

(1)证明：如图1中，

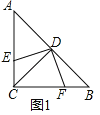
∵∠ACB＝90°，CD⊥AB，

∴∠ACD+∠A＝∠B+∠A＝90°，

∴∠ACD＝∠B，

∵DE⊥DF，

∴∠EDF＝∠CDB＝90°，

∴∠CDE＝∠BDF，

∴△DEC∽△DFB.

(2)结论成立.

理由：如图2中，

∵∠ACB＝90°，CD⊥AB，

∴∠ACD+∠A＝∠B+∠A＝90°，

∴∠ACD＝∠B，

∴∠DCE＝∠A+90°，

∠DBF=∠A+90°，，

∴∠DCE＝∠DBF，

∵DE⊥DF，

∴∠EDF＝∠CDB＝90°，

∴∠CDE＝∠BDF，

∴△DEC∽△DFB.

(3)∵∠ACD＝∠B，∠ADC＝∠BDC，

∴△ADC∽△CDB

∴＝＝，

由(2)有，△CDE∽△BDF，

∵＝＝，

∴＝＝＝，

∴CF＝2AE，

在Rt△DEF中，DE＝2，DF＝4，

∴EF＝＝＝2，

①当E在线段AC上时，在Rt△CEF中，CF＝2AE＝2(AC﹣CE)＝2(﹣CE)，EF＝2，

根据勾股定理得，CE2+CF2＝EF2，

∴CE2+[2(﹣CE)]2＝40

∴CE＝2，或CE＝﹣（舍）

而AC＝＜CE，

∴此种情况不存在，

②当E在AC延长线上时，

在Rt△CEF中，CF＝2AE＝2(AC+CE)＝2(+CE)，EF＝2，

根据勾股定理得，CE2+CF2＝EF2，

∴CE2+[2(+CE)]2＝40，

∴CE＝，或CE＝﹣2(舍)，

③如图3中，当点E在CA延长线上时，

CF＝2AE＝2(CE﹣AC)＝2(CE﹣)，EF＝2，

根据勾股定理得，CE2+CF2＝EF2，

∴CE2+[2(CE﹣)]2＝40，

∴CE＝2，或CE＝﹣(舍)

即：CE＝2或CE＝.