ЬтФПФкШн
ЁОЬтФПЁПФГЩЬГЁЯњЪлвЛХњГФЩРЃЌЦНОљУПЬьПЩЪлГі![]() МўЃЌУПМўгЏРћ
МўЃЌУПМўгЏРћ![]() дЊЃЎЮЊСЫРЉДѓЯњЪлЃЌдіМггЏРћЃЌЩЬГЁОіЖЈВЩШЁЪЪЕБЕФНЕМлДыЪЉЃЎОЕїВщЗЂЯжЃЌдквЛЖЈЗЖЮЇФкЃЌГФЩРЕФЕЅМлУПЯТНЕ
дЊЃЎЮЊСЫРЉДѓЯњЪлЃЌдіМггЏРћЃЌЩЬГЁОіЖЈВЩШЁЪЪЕБЕФНЕМлДыЪЉЃЎОЕїВщЗЂЯжЃЌдквЛЖЈЗЖЮЇФкЃЌГФЩРЕФЕЅМлУПЯТНЕ![]() дЊЃЌЩЬГЁЦНОљУПЬьПЩЖрЪлГі
дЊЃЌЩЬГЁЦНОљУПЬьПЩЖрЪлГі![]() МўЃЎ
МўЃЎ
![]() ШчЙћЩЬГЁЭЈЙ§ЯњЪлетХњГФЩРУПЬьЛёРћ
ШчЙћЩЬГЁЭЈЙ§ЯњЪлетХњГФЩРУПЬьЛёРћ![]() дЊЃЌФЧУДГФЩРЕФЕЅМлгІЯТНЕЖрЩйдЊЃП
дЊЃЌФЧУДГФЩРЕФЕЅМлгІЯТНЕЖрЩйдЊЃП
![]() ЕБУПМўГФЩРЕФЕЅМлЯТНЕЖрЩйдЊЪБЃЌУПЬьЭЈЙ§ЯњЪлГФЩРЛёЕУЕФРћШѓзюДѓЃПзюДѓРћШѓЮЊЖрЩйдЊЃП
ЕБУПМўГФЩРЕФЕЅМлЯТНЕЖрЩйдЊЪБЃЌУПЬьЭЈЙ§ЯњЪлГФЩРЛёЕУЕФРћШѓзюДѓЃПзюДѓРћШѓЮЊЖрЩйдЊЃП
ЁОД№АИЁПЃЈ1ЃЉУПМўГФЩРгІНЕ20дЊЃЛ
ЃЈ2ЃЉУПМўГФЩРНЕМл15дЊЪБЃЌЩЬГЁЦНОљУПЬьгЎРћзюЖрЃЌзюДѓРћШѓЮЊ1250дЊЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнзмРћШѓ=УПМўРћШѓЁСЯњЪлСПСаЗНГЬЃЌЧѓНтМДПЩЃЛ
ЃЈ2ЃЉЩшУПЬьРћШѓЮЊwдЊЃЌУПМўГФЩРгІНЕМлxдЊЃЌИљОнЬтвтПЩЕУРћШѓБэДяЪНЃЌдЫгУКЏЪ§ЕФаджЪЧѓзюжЕЃЎ
ЃЈ1ЃЉЩшГФЩРЕФЕЅМлгІЯТНЕxдЊЃЌгЩЬтвтЕУЃК
1200=ЃЈ20+2xЃЉЁСЃЈ40ЉxЃЉ
НтЕУЃКx=20Лђ10ЃЌЁрУПЬьПЩЪлГіЃЈ20+2xЃЉ=60Лђ40МўЃЛ
ОМьбщЃЌx=20Лђ10ЖМЗћКЯЬтвтЃЎ
ЁпЮЊСЫРЉДѓЯњЪлЃЌдіМггЏРћЃЌЁрxгІШЁ20дЊЃЎ
Д№ЃКГФЩРЕФЕЅМлгІЯТНЕ20дЊЃЎ
ЃЈ2ЃЉw=ЃЈ40ЉxЃЉЃЈ20+2xЃЉ=Љ2x2+60x+800=Љ2ЃЈxЉ15ЃЉ2+1250
ЕБx=15ЪБЃЌгЏРћзюЖрЮЊ1250дЊЃЎ

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИЁОЬтФПЁПМзЁЂввСНУћЖгдБЕФ10ДЮЩфЛїбЕСЗЃЌГЩМЈЗжБ№БЛжЦГЩЯТСаСНИіЭГМЦЭМ.
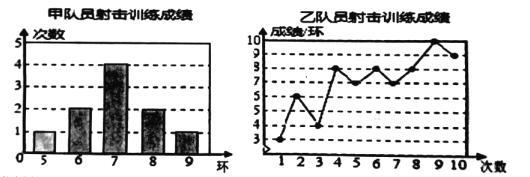
ВЂећРэЗжЮіЪ§ОнШчЯТБэЃК
ЦНОљГЩМЈ/ЛЗ | жаЮЛЪ§/ЛЗ | жкЪ§/ЛЗ | ЗНВю | |
Мз |
| 7 | 7 | 1.2 |
вв | 7 |
| 8 |
|
ЃЈ1ЃЉЧѓ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЗжБ№дЫгУБэжаЕФЫФИіЭГМЦСПЃЌМђвЊЗжЮіетСНУћЖгдБЕФЩфЛїбЕСЗГЩМЈ.ШєбЁХЩЦфжавЛУћВЮШќЃЌФуШЯЮЊгІбЁФФУћЖгдБЃП