��Ŀ����
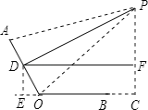
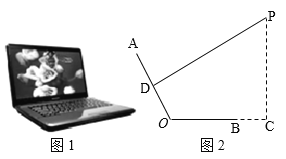
����Ŀ����ͼ1��һ̨������ˮƽ�����ϵıʼDZ����ԣ��������������ͼ2��ʾ�ļ���ͼ��.����ʾ��AO�����BO����Ϊ24cm����PΪ�۾�����λ�ã�DΪAO���е㣬����PD����PD��AO����ʱ��PΪ����ӽǣ�����C��OB���ӳ����ϣ�PC��BC��BC��12cm.
��1����PA��45cmʱ����PC�ij���
��2������AOC��115��ʱ���߶�PC�ij��ȣ�1�����߶�PC�ij��������Ǽ�С����ͨ������˵�����������ȷ��0.1cm��sin65���0.91��cos65���0.42��tan65���2.14��sin25���0.42��cos25���0.91��tan25���0.47��.
���𰸡���1��27![]() ��2������
��2������
��������
��1����PA��45cmʱ������PO�����ù��ɶ������PC��
��2������AOC��115��ʱ������D��DE��OC��BO���ӳ�����E������D��DF��PC������ΪF������������Ǻ����ֱ����FC��PF���ɵõ���.
�⣺��1����PA��45cmʱ������PO��
��DΪAO���е㣬��PD��AO��
��PO��45cm.
��BO��24cm��BC��12cm����C��90�㣬
��OC��OB+BC��36cm��PC��![]() ��27cm��
��27cm��
��2������AOC��115��ʱ������D��DE��OC��BO���ӳ�����E������D��DF��PC������ΪF��
���ı���DECF�Ǿ��Σ�
��Rt��DOE��
�ߡ�AOE��65�㣬DO��![]() AO��12��
AO��12��
��DE��DOsin65�㣽12��0.91��10.92��EO��DO cos65�㣽12��0.42=5.04��
��FC��DE��10.92��DF��EC��EO+BO+BC��5.04+24+12��41.04��
��Rt��PDF��
�ߡ�PDF��25�㣬
��PF��DFtan25�㣽41.04��0.47��19.29��
��PC��PF+FC��19.29+10.92��30.2��27.
���߶�PC����������.